Adjust Your Expectations

Or: What's brain damage got to do with it?

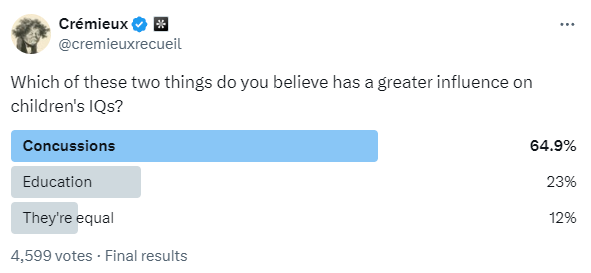
I polled Twitter, a Discord convenience sample, and a sample from Qualtrics. I wanted to know what people thought would have a bigger impact on children’s IQs: getting a concussion or an education.¹ The answer people provided was clear support for the belief that concussions are more important than education across each sample.

Link

People “know” that concussions have a verifiable effect on the brain, so they imagine concussions must do something, whereas many people also think of IQ as a relatively hardwired psychological trait that education is unlikely to affect.²

You may be shocked to learn that the literature on concussions and other minor traumatic brain injuries—mTBIs—includes a lot of disagreement about whether mTBIs impact IQs.

Several studies have found support for the common sense conclusion that mTBIs reduce IQs or otherwise induce cognitive impairments.

Wrightson, McGinn and Gronwall took 78 preschoolers admitted to emergency departments with mild head injuries not requiring readmission for observation and compared them with a sample of 86 children who were admitted to the emergency department for minor injuries elsewhere on the body. Kids were cognitively tested three times in the year after injury and again when they were six-and-a-half years old. There were no tests prior to injury.

Shortly after injury, there were no significant differences in performance on the Reynell Developmental Language Scales or any of the ten subtests of the Illinois Test of Psycholinguistic Abilities (ITPA).³ At the six- and twelve-month post-admission testings, there were two significant differences and they were both on scores for the ITPA’s visual closure subtest, such that the control group scored a bit higher. At 6.5 years old, the test battery included the ITPA, the Neale Analysis of Reading Ability, a test of letter knowledge and writing, the Wechsler Intelligence Scale for Children’s coding subtest, a verbal memory passage, a visual memory test, a paired-associated learning task, and the Frostig Developmental Test of Visual Perception. In other words, these kids took a lot of test, but despite taking so many tests, the only significant difference was in the ITPA’s visual closure subtest and it was marginally significant before correcting for multiple comparisons (p = 0.015).

Yeates et al. compared 186 8-to-15 year-old children with mTBIs to 99 with orthopedic injuries who were admitted to two hospitals in Columbus and Cleveland, Ohio. The children were assessed no later than three weeks after their injuries through parental reports about children’s pre- and post-injury symptoms and behavior. Parents reported on cognitive and somatic symptoms, quality of life, and whether children had special accommodations in school.

A year after injury, the mTBI-affected children there were some (frequently marginal) increases in symptoms. Unfortunately, some of the reporting in this study was frustratingly unclear. For example, information on educational accommodations wasn’t presented, but information on the relationship between accommodations and reported increases in symptoms was. IQ was also measured at the initial assessment, but we don’t see any reporting on whether that was measured at or changed by the follow-up.

Ransom et al. assessed the symptoms of 359 students aged 5 to 18 who had sustained a concussion and whose parents had reported academic concerns and problems on a school questionnaire within four weeks after an injury had occurred. Kids were classified as recovered or symptomatic and reports about the symptomatic kids were worse than the ones about the kids who were felt to be recovered.

Several studies have also failed to find support for the common sense conclusion.

Bijur, Haslum and Golding used data from a longitudinal study including some 13,000 British children over several years. They compared the IQ scores of 114 children who had been given ambulatory care or received a hospital admission for a mild hear injury with 601 who broke a limb, 605 who suffered a laceration, 136 who were burned, and 1,726 who were uninjured between assessments given at ages 5 and 10. At the age 10 assessment, children’s scores were adjusted for the scores they obtained at age 5. The kids who had suffered head injuries were not cognitively distinguishable after this adjustment, but they did have four-tenths of a standard deviation higher hyperactivity scores. Otherwise, they weren’t all that differentiated.

Light et al. compared 119 children aged 8 to 16 with head injuries with 114 children with other injuries and 106 without any injuries. I like to think of this tripartite comparison like the quasi-experimental version of having an active and a passive control group. The thing that makes this possible is that there are pre-injury and one year post-injury results for all of the children. The nature of the sample was such that the researchers found the kids by scouring emergency room records for kids who were residents of LA, Riverside, or Orange County who also had records based on their school attendance that the researchers could match them to. The matching procedure was pretty involved, making the quality of the matching between the samples exceptional.

There didn’t seem to be any changes in group differences in measures of behavioral problems, school grades, or test scores after injury. That result was thus very similar to the result provided by Russell et al., who asked 124 students—92 of whom had sports-related concussions and 32 of whom had sports-related fractures—to submit pre- and post-injury report cards. Both groups of students experienced similar magnitudes of nonsignificant decreases in grades following their injuries.

The common sense-affirming studies are shockingly uninformative about the effects of mTBIs. They frequently feature small samples, poor and subjective measurements and classifications, and lots of tests only to find few and generally marginally significant differences that typically wouldn’t survive reasonable corrections for multiple comparisons. The common sense-defying studies on the other hand appeared to be better representations of the wider literature. Quoting from Carroll et al.’s meta-analysis of 120 different studies of post-mTBI prognosis:

There was consistent and methodologically sound evidence that children's prognosis after mild traumatic brain injury is good, with quick resolution of symptoms and little evidence of residual cognitive, behavioural or academic deficits. For adults, cognitive deficits and symptoms are common in the acute stage, and the majority of studies report recovery for most within 3-12 months. Where symptoms persist, compensation/litigation is a factor, but there is little consistent evidence for other predictors.

And the most important part:

The literature on this area is of varying quality and causal inferences are often mistakenly drawn from cross-sectional studies.

The reason is well-known: selection! The authors warned of confounding factors like “pre-injury symptoms and personality characteristics, pre- and post-injury psychological distress, factors related to litigation and compensation and pain associated with injuries to other parts of the body,” among other things.

The most common way to deal with confounding in the mTBI literature was to look for good comparison groups. The best study doing that which I’m aware of is by Ware et al., and it’s fairly new.

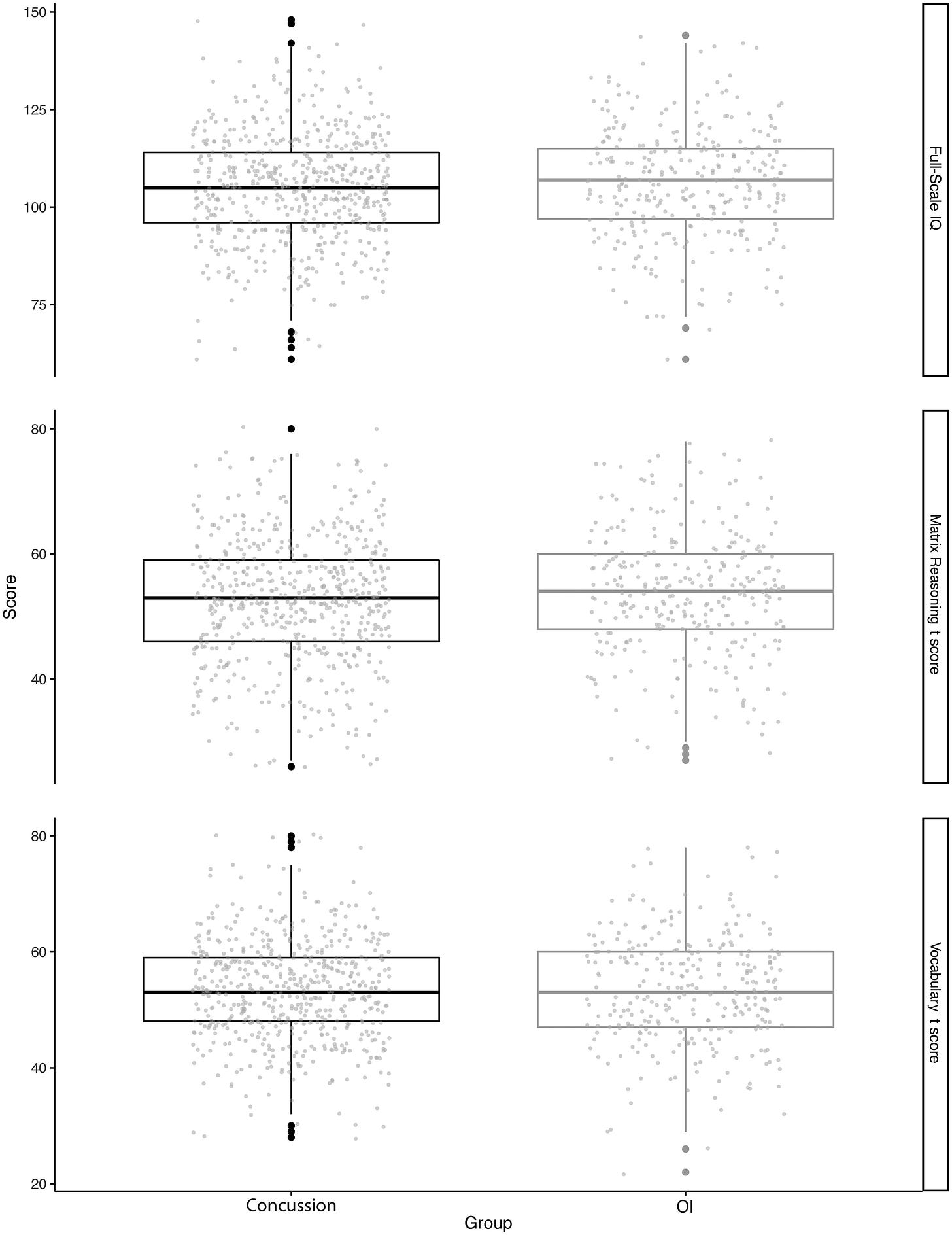
In Ware et al.’s study, they recruited 866 children aged 8 to almost 17 years of age from two retrospective cohort studies at children’s hospitals, two of which were in the U.S. and five of which were in Canada.⁴ The kids had either an mTBI or an orthopedic injury. They completed IQ tests three to eighteen days after being injured in the U.S. samples and three months after being injured in the Canadian samples.

The statistical attention to detail in this study was refreshing. The authors included power analyses, used linear models, Bayesian methods, and they even tested for measurement invariance—remarkably, they even tested for it correctly!⁵ The linear models are practically unnecessary because the result hits you between the eyes: whether in full-scale IQ scores, matrix reasoning, or vocabulary, there wasn’t much worth caring about.

Ware et al. 2023, Figure 2

The differences in full-scale IQ scores (p = 0.05) and matrix reasoning (0.02) were not really significant or marginally significant, respectively. The difference in vocabulary was simply not significant (0.42). Bayes factors were computed for the full-scale IQ scores (0.10), vocabulary (0.02), and matrix reasoning (0.23), and they were consistent with strong evidence against an effect, very strong evidence against an effect, and moderate evidence against an effect, respectively.

The part of the study that really excited me was that they tested for measurement invariance with respect to both subtests and they found that every model-fitting stage fit well, from configural all the way through the structural modeling stages for the variances, relationships between the subtests, and the latent mean.

In other words, the groups were completely cognitively comparable and there just wasn’t any evidence for acute effects of pediatric mTBIs on IQs despite adequate power to detect fairly small effects.

This study was good but it was also far from perfect. The matching might have been subpar—who’s to say mTBIs and other orthopedic injuries actually affect comparable groups of people? The cognitive test also left a bit to be desired, because it only included two subtests and who’s to say mTBIs don’t tend to affect some other, specific facet of cognition?⁶ And hey, what if the impacts are only felt over much longer time intervals than the post-acute period?

---

Unequal Injuries, Unequal Learning

The cleanest solution to the comparison group issue for mTBIs is to use individuals as their own comparisons in longitudinal data or a design that amounts to doing the same thing. The easiest way to get long-term pre- and post-injury longitudinal data is to use school records that can be matched with hospital records in a system where both school and healthcare are socialized.

The easiest way to obviate concerns about the things the tests measure is to… well, there’s just one way around that. If we want to know if mTBIs have effects on, say, spatial or mathematical or verbal ability specifically, the only way to tell involves the use of many different types of tests. Realistically, that’s not going to get credibly assessed any time soon, so studies will have to stick to testing two other things that are still very meaningful: whether general intelligence and socially significant test results are affected.⁷

The Scandinavian countries have populations that trust their governments and they have governments efficient enough to have population registers linking together the required data. The best test of what effect mTBIs have on cognitive development comes from Denmark, where this data has been put to use for this exact purpose.

The design is ingenious. It looks like this:

Blaabæk, Andersen and Fallesen 2024, Fig. 1

This is a difference-in-differences design that employs multiple time periods. In each grade, the effect is estimated using children who have an mTBI in later grades so that the counterfactual trend can be inferred, hence “for each grade, we compare the change from the previous period to the same change of the lower lines that represent children who are not yet treated.” Weigh each cohort’s estimates and you get the average treatment effect on the treated in the year of the treatment which is, in this case, the year of getting an mTBI.

The baseline data indicates that getting an mTBI is selective with respect to parental education (ISCED-coded) and earnings: poorer families with less education are also ones where kids are more likely to get mTBIs, and their kids average lower test scores.

Blaabæk, Andersen and Fallesen 2024, Fig. 2

The test in question is a high-quality mandatory reading test and scores on it are significantly negatively correlated with reading test scores. Controlling for family earnings, parental education, sex, region of residence, parental Western or non-Western origin, other injuries, and a child’s grade, about half of the relationship goes away. Turning this into a sibling comparison, the effect becomes nonsignificant.

Clearly confounding matters when it comes to mTBIs. The difference-in-differences estimates are thus clearly important. They suggest no effect for mTBIs within the year before testing.⁸

At the most extreme end of the confidence intervals shown here, the effect of an mTBI could be equal to 8% of a year of typical learning progression.

Getting an mTBI is selective and associated with worse academic performance because poorer performers are more likely to get mTBIs rather than that mTBIs cause the deficits associated with them. Or stated differently, due to the selectiveness of getting an mTBI, they could, at most, socially stratify educational achievement by a tiny amount:

Fallesen et al. (2022) identify one year of learning on the same national reading tests as 0.55. If we relate the educational gradient in mTBIs (−0.012) to the most extreme negative end of the confidence band from the main model (−0.043), mTBIs would at most contribute 0.05% of a standard deviation to the gap between ISCED 5–20 and 50+ families. This equates to just 0.06% of the raw gap of 85% of a standard deviation.

---

If Not Concussions, Why Education?

One-off mTBIs don’t contribute to variation in cognitive ability in the general population and they don’t contribute to the social stratification of the educational experience. This isn’t to say that TBIs that aren’t just concussions have no effect, that some mTBIs don’t have an effect, or that there’s no cumulative impact of multiple mTBIs, but it is to say that just because something obviously impacts the brain doesn’t mean that it affects every variable that sounds ‘brainy,’ IQ included.

When polled, people were more willing to believe that concussions have an effect on IQs than education does. That opens up an important question: because mTBIs don’t seem to average an effect, how should we adjust our estimate of the effect of education on IQs?

---

Something’s Missing

If we want to mentally adjust the effect of education on IQs based on a prior we have about concussions, we need to know how large the education effect is reported to be. Unfortunately, there’s a lot missing from current estimates of the effects of education.

In a previous article, I mentioned three commonly used designs for estimating the effect of education on individual’s IQs. These designs

• Use longitudinal data to estimate the effect of another year of education

• Use policy changes to estimate the effect of a year of basic education extension⁹

• Use school age cutoffs to estimate the effect of starting education a year earlier.

The longitudinal studies are not natural experiments, but they’re probably the best we have for

• Estimating the effects of higher education rather than basic education¹⁰

• Establishing the nature of diminishing returns.

Diminishing returns are intuitive. If they didn’t exist, people could continue with education for their whole lives, resulting in higher and higher scores on affected tests. The notion is fanciful and it implies a lot of implausible things about the scales of scores and people’s ability to improve without directly training for a test. But, it’s barely been assessed. Because of the potential importance of diminishing returns, it’s surprising that so few studies have tried to estimate whether and when they’re present.

---

Reanalysis of a Scottish Cohort

When using longitudinal data to estimate the effect of another year of education, we run into a problem: more intelligent people are more likely to attain higher levels of education. In a word, there’s selection. The longitudinal studies deal with selection by controlling for an earlier measure of intelligence. Unfortunately, this results in overestimated effects of education when the childhood measures contain measurement error, resulting in the selection effect being partially attributed to education.

For Ritchie and Tucker-Drob’s meta-analysis of the effects of education on IQ, they conducted a novel one of these studies using the 1970 British Cohort Study (BCS). In the BCS, participants took a high-quality intelligence test when they were ten years old and they took a numeracy test when they were thirty-four. A single numeracy measurement is not ideal. Only having that available means several things. It means that the problem of a single measure’s reliability can’t be corrected by using a latent variable model. It also means that general intelligence cannot be modeled in the follow-up and—without items—bias cannot be assessed, so to do this analysis requires assuming the numeracy measure is a sufficient proxy for intelligence.¹¹

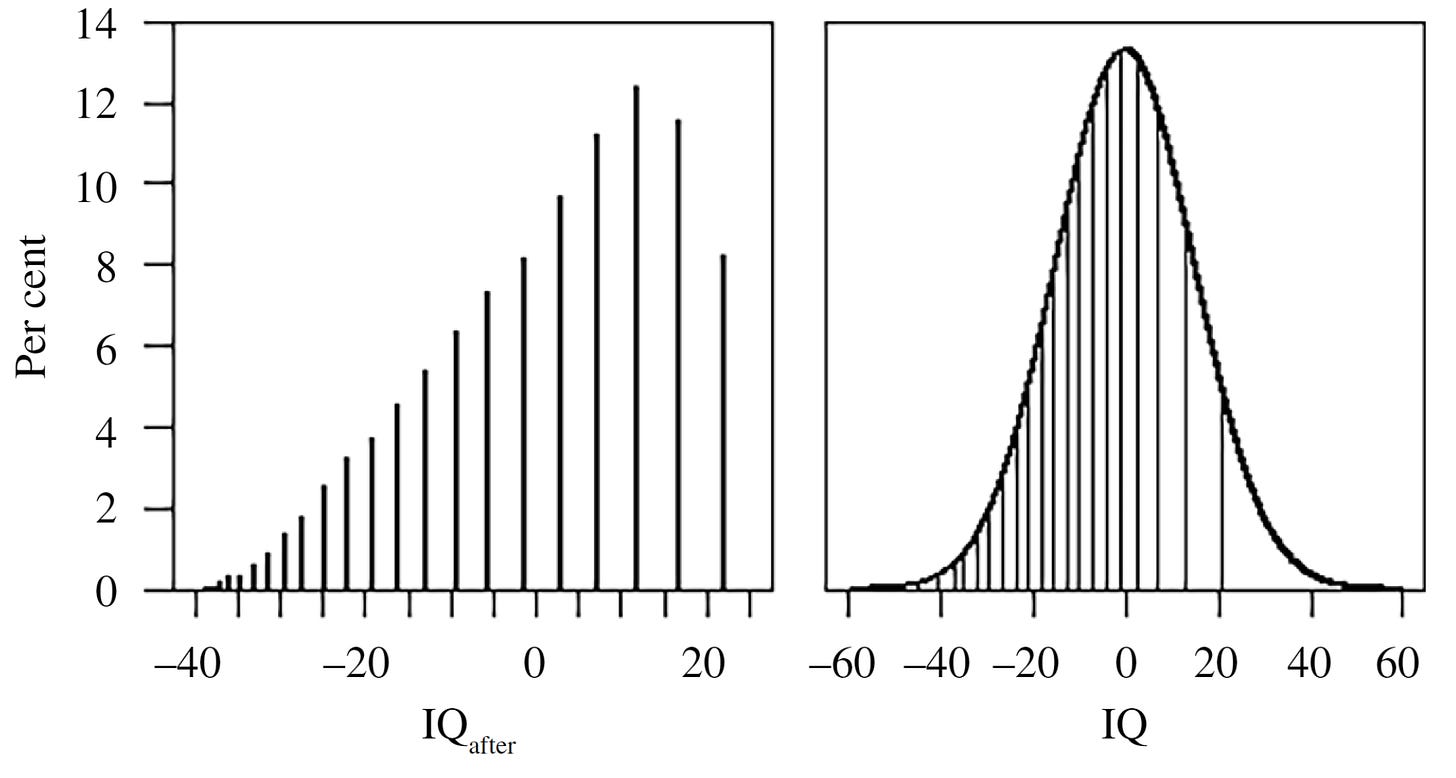
With that assumption in hand, there are still problems. In a new reanalysis of Ritchie and Tucker-Drob’s BCS analysis, Eriksson et al. showed that the form of the numeracy measure is strongly discretized and it has range restriction issues that give it a left skew. A ceiling can readily lead to underestimating the positive effects of education.

Eriksson et al. 2024, Figure 1

On the left, you can see the distribution of the numeracy measure Ritchie and Tucker-Drob used, versus where those points correspond to on a normal distribution on the right. If discretization weren’t so problematic, the solution to this ceiling effect would be to use a Tobit regression. The reason that won’t work is visible if you look at the figure on the right. For example, the highest and the second-highest numeracy scores correspond to considerably different ranges in IQ scores—the distances between discrete points aren’t equally meaningful, so corrections that don’t or can’t account for that are ruled out.

To overcome this issue, Eriksson et al. leveraged the fact that intelligence is normally distributed in the general population, forcing the study population’s distribution to be more like that. They started off by using the same method used by Ritchie and Tucker-Drob (covariate method). They then corrected for different reliability values in an error-in-variables model. Finally, they used a fixed-point iteration simulation approach to correct those error-in-variables estimates for dependencies between their ultimate error term and their initial independent variables.

The point is to estimate b_{HE}—the effect of another year of higher education—and b_{start}, the contribution of IQ prior to higher education on IQ after it’s completed. This is how the model looks:

Eriksson et al. 2024, Figure 2

The result is evidently highly dependent on the level of reliability. Using Ritchie and Tucker-Drob’s specification, b_{HE} was estimated at 0.86. Stated theoretically, that’s “An additional year of education results in a further 0.86 IQ points.” The value for b_{start} looked comparatively weak, at just 0.47. But once measurement error corrections come into play, the apparent effect of education is greatly reduced and the stability of IQ over time is considerably increased.¹²

The point of this section wasn’t to talk about issues with estimating the effects of education in general, it was to talk about diminishing returns. Getting to that is why the simulation is key: it allows assessing whether there are differences in expected mean IQs in real data versus in the linear model, over a certain number of years of completed higher education, with the other corrections in place.

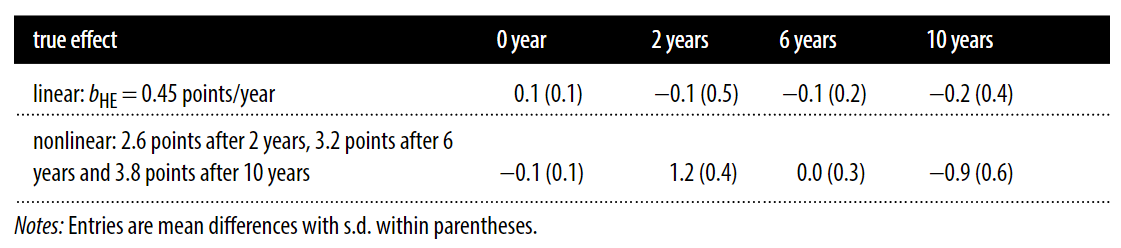
With simulated data, nonlinearity leads to a pattern of differences between true mean IQs for given levels of higher education experience and the ones that are estimated in the final iteration of the iterated simulation model like so:

Eriksson et al. 2024, Table 1

The pattern that emerges under nonlinearity is one in which IQs are overpredicted for individuals with moderate amounts of educational experience and accurate prediction happens for individuals with no or a large amount of experience. In the real data, a pattern of early overprediction is exactly what shows up.

The true effect of higher education may very well be nonlinear and, after a few years in school, attendance might not offer any more IQ benefits.

---

What Next?

Since it’s now been established that the effects of education on IQ may be nonlinear, it serves to reason that the studies estimating that effect need to be redone to account for that possibility. With enough reanalysis, it might be possible to figure out whether there are cognitive benefits to higher education, and if so, how large they are and how much effort is required to obtain them. Until those reanalyses have been run, we should probably abstain from thinking too highly of the existing literature. The magnitude of the correction for reliability alone in the BCS was such that it halved the purported effect of higher education. If that’s the sort of reduction we can expect across the board, then the need for reevaluation is serious.

For a lot of people, I imagine this result still doesn’t add up. After all, they thought concussions would matter more than education, but two years in higher education looks to net a handful of points on an IQ test and the average effect of a concussion is approximately nothing. That’s not to say that mTBIs aren’t bad or that education makes people more intelligent—more extensive modeling is still required to say that—but it is to say this: we should adjust our expectations.

1. Some people on Twitter were confused about my wording, which is understandable given the medium’s required brevity, but I still achieved similar results through Discord and Qualtrics. The wording was clearer in the Discord and Qualtrics samples and the point of the Qualtrics sample was not to ask this question in particular.

Since posting the Qualtrics, Discord, and Twitter results on Twitter (now deleted), another large account reached out to help with replication. If you would also like to help me assess the replicability of Twitter polls and you have a large following (>=50,000 followers), message me.

The wording confusion had to do with whether the question was asking about the treatment effect of an education versus a concussion or the effect on the population’s mean IQ level. It stands to reason that, on the population level, the impact of an education would be larger even if its impact is smaller for individuals since educations are much more common than concussions. The question referred to the treatment effect.

2. It’s rare for people to think about what IQ scores are or what they mean. Most people default to thinking of IQ scores as unconditional proxies for intelligence unless explicitly prompted otherwise. Consider literacy. Without it, a verbal IQ test would produce invalid results. Therefore, education is, at least in some cases, necessary to produce a valid IQ score. Similarly, increased education may result in benefits to IQ scores that aren’t benefits to intelligence, through enhancing narrow skills involved in testing, affecting specific abilities, or biasing tests. I have written about this before.

3. These are auditory reception, visual reception, visual sequential memory, auditory association, auditory memory, visual association, visual closure, verbal expression, grammatical closure, and manual expression. The paper contains descriptions of each subtest for those interested.

4. This detail is important—multi-center/multi-site RCTs replicate better than single-center/single-site RCTs, and single-center RCTs often fail to be confirmed by subsequent multi-center RCTs for reasons that do not appear to be down to identifiable method-related variance but, instead, to single-site idiosyncrasies that aren’t reliable.

In some fields, people have argued that this is due to things like a failure to standardize protocols across sites, heterogeneity in treatment and measurement effort and quality, and more, but, at least in medicine, these sorts of complaints are rarely true. In what I consider to be a very revealing case, Roy Baumeister even claimed that multi-site replication efforts are biased towards failure. I don’t agree in general, but maybe he’s right about his field (social psychology). Having known some of the people involved in Many Labs, every one of them that I’m acquainted with doesn’t seem like they would be the sorts of people to intentionally or negligently tank replication efforts, so I’ll just register here that I don’t give much credit to Baumeister’s arguments or remarks about multi-site replications, but I’m more than open to him presenting credible evidence that multi-site replications are wracked with problems, if he (or anyone else for that matter) can find it.

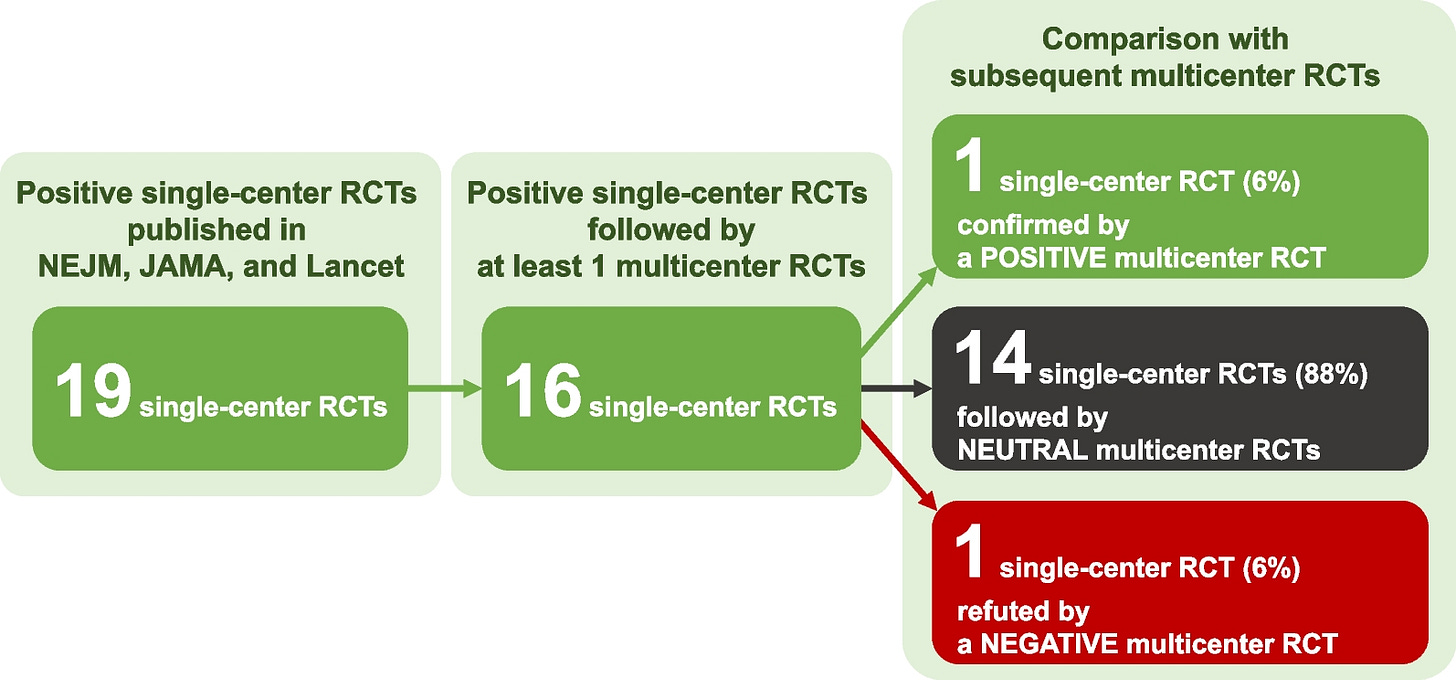
My most recent reminder of the fact that we need multi-site RCTs Kotani et al. These authors looked at the replicability of mortality reductions for critically ill patients shown in nineteen different single-center RCTs. Sixteen of these studies had a multi-site replication, but the results were disappointing: one study significantly replicated, one study had its findings significantly reversed, and fourteen studies came back null. That’s a 1/16 replication rate!

Kotani et al. 2023, Fig. 2

Despite only one replicating, fourteen of them were cited at least once in clinical guidelines, with six of those citations remaining in current suggestions for use, two now being cited to indicate insufficient evidence, and another six now being omitted or explicitly contraindicated. So these failures might still be having impacts.

On a similar note, subgroup analyses of RCTs are common. They are frequently used to make an RCT that failed to achieve significant results for its primary endpoints seem like it found something significant despite failing. A 2017 review suggested that less than half of RCT subgroup analyses were supported by their own data (46 of 117). In that analysis, few of those internally-supported subgroup analyses were later given corroboration attempts (5 of 46), and only one of those corroboration attempts came with a significant p-value. All-in-all, subgroup findings in RCTs—as in many places—tend to be spurious and though many are presented, remarkably few are explicitly tested.

But people respect these results and have all-too-frequently taken them seriously, so imagine how much havoc these have wrought on clinical guidelines.

5. It’s remarkable because an inappropriate test for measurement invariance is much more common than a good test.

6. There’s one meta-analysis of the relationship between g-loadings and the effects of traumatic brain injuries—not mTBIs per se—and it indicates no correlation, so the effects are not apparently associated with or inversely associated with g and they may, in fact, be diffuse. For want of causality, I’ll postscript with the phrase “for whatever that’s worth.”

The other studies cited here also do not seem to show results consistent with mTBIs tending to cause specific types of cognitive deficits.

7. An effect on general intelligence can be suggested with a handful of tests and excluded with just one test. Credible confirmation of a general effect can be difficult because of issues with content being insufficiently broad in a given test battery, but it’s arguably achievable with an adequately theoretically justified test, like one involving a standard intelligence testing battery that has diverse content, such as the Wechsler Adult Intelligence Scale or the Woodcock-Johnson.

A socially significant test is one that is used for selection or screening in some other facet of life, such as a civil service examination that must be passed in order to secure a job in the civil services, an exam to qualify for entry to an elite school, or an exam to be able to pursue higher education at all.

Many tests used regularly in education may not themselves by socially significant, but they often contain the same content as and thus serve in the role of adequate proxies for actually socially significant tests. This is probably why it’s well-known that high- and low-stakes test results are highly correlated! In the case of end-of-course exams, I would argue that they’re frequently high-stakes since failure can necessitate being held back a grade, which very few people actually want to happen to them.

In the Danish data referenced in this post, the tests being used are mandatory for children in public schools unless they are deemed “unfit” to take the test.

8. The estimate for an mTBI within twelve months is the illustrated 0.000, for six months it’s 0.012 (i.e., ‘mTBIs improve reading scores’), for three months it’s 0.075, and for one month, it’s -0.005. None of these estimates are anywhere near significant.

9. Or, in a few cases, reductions.

Leveraging policy changes that affect the amount of education many people go through can be ideal from a design point of view. The change supplies useful exogenous variation on a particular margin that might be of interest, but quantifying the effects of these changes can be unwieldy and the studies are usually not readily replicable due to their nature as studies of a shift in policy. From a psychometric point of view, policy changes tend to be less than ideal since they usually don’t permit figuring out sources of stability and change in scores and their chance nature means they tend to come with subpar measures.

10. People generally agree that basic education should have a larger effect on IQs than higher education, in part because of the necessity for performance, in part because of developmental timing, and in part because of diminishing returns, among other possibilities.

11. It might be inappropriate in terms of the effect size produced and for determining the specificity of the effect. That is, a numeracy test might be more or less affected than tests with other content types tend to be, and the result based on a numeracy test alone could only coincidentally correspond with the effect on a latent variable from a larger battery.

The effect size arrived at here using Ritchie and Tucker-Drob’s method delivered an effect that was similar to their meta-analytic estimate, so this assumption is probably not too bad.

12. The use of a single measure leads to instability still being greatly overstated even accounting for measurement error, because g averages more stable than specific skills.