Don't Ignore Your Intercepts

Failing to understand this simple methodological issue undermines theoretical reasoning

The relationship between brain size and intelligence is a correlation of about 0.4, and the relationship is causal. Here’s some simulated data to illustrate that relationship:

Now that we know brain size and intelligence are related, let’s couple it with some other information. For example, women average smaller brains than men. The difference is substantial and it holds up to correction for body size. If women have 1 SD smaller brains than males, and the correlation between intelligence and brain size is 0.4, then women should have 0.4 SDs lower intelligence. But in reality, women and men tend to have the same levels of measured intelligence. Thus, the graph above split by sex usually looks like this:

Because intelligence is equal by sex and brain sizes are unequal, the intercept in this regression is biased, meaning that at all levels of intelligence, men tend to have larger brains than women.

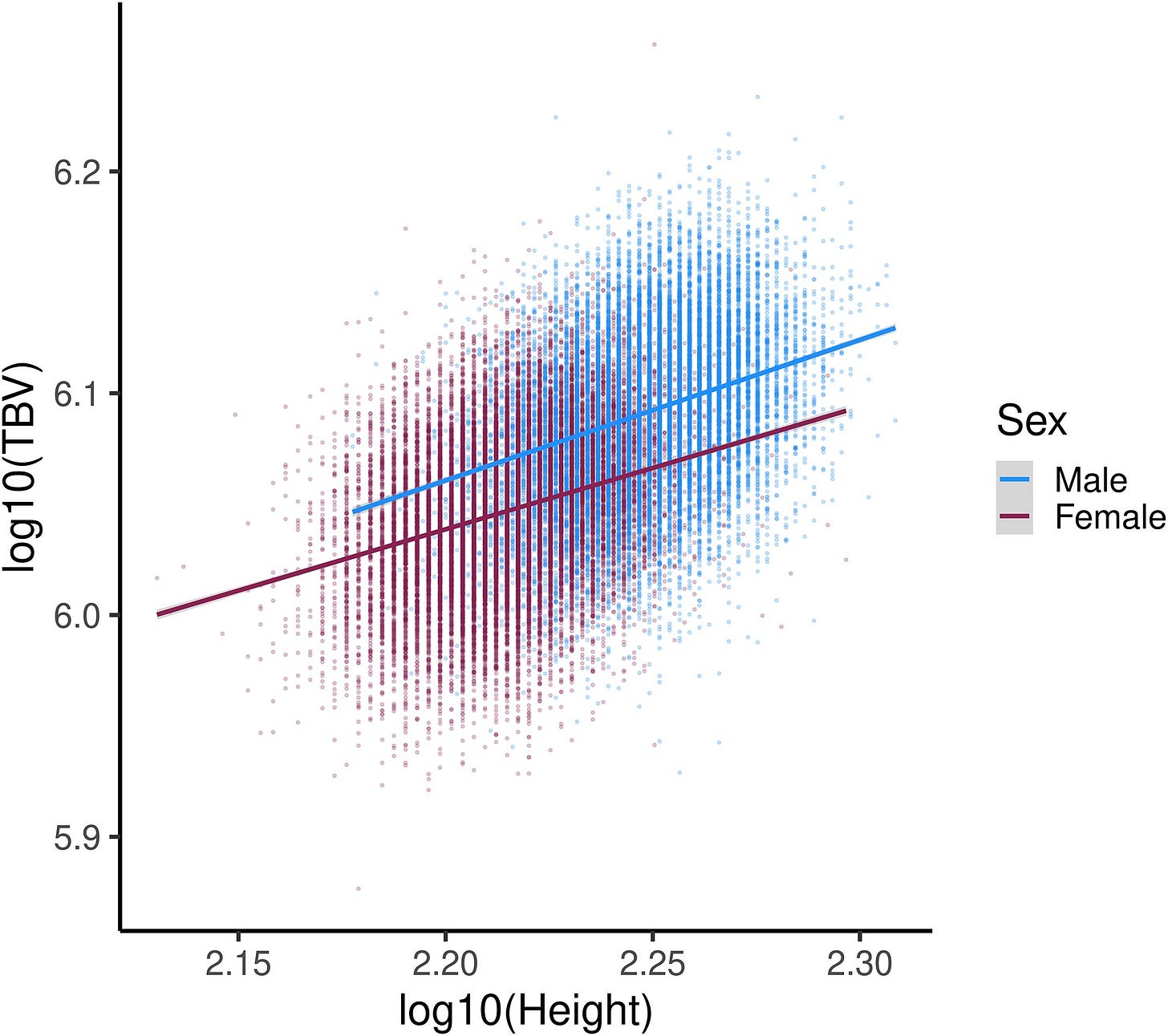
On a less contentious note, both height and brain size are related—as you might expect given height scales up the body. Women have both shorter statures and smaller brains than men; it’s only natural to assume that the discrepancy in brain sizes is down to the well-known difference in heights. But, as with intelligence and brain size, when we plot the two next to one another, we see a difference in intercepts: at all heights, men tend to have larger brains!

Williams et al. 2021, Fig. 1

Substantively, the male brain size “advantage”¹ is due to something that varies between sexes, such that men have brains that are less efficient pound-per-pound compared to women, but brains that are nevertheless much larger. I could provide more detail as to what that “something” is, but that’s not the point of this post. What I really want to talk about is intercept-free reasoning.

The notion that women have smaller brains and thus they should be less intelligent is not supported once we take into account that the intercepts vary. Reasoning from the slope alone (i.e., r = 0.4, d_{brain size} = 1, therefore, d_{intelligence} = 0.4) makes sense and is a form of reasoning that is often valid, but it wasn’t valid in this case, because of the aforementioned finding that at all levels of intelligence, men tend to have larger brains. That boost at all levels is the unacknowledged difference in the intercepts that renders the slope-based reasoning invalid, either in full or in part.

Here’s another example.

Within countries, races, sexes, etc., the relationship between height and intelligence is positive. Within sexes in a given race in a given country, the relationship between height and income is also positive. Some extreme examples of this relationship are well-known, such as that U.S. presidents and Fortune 500 CEOs tend to be taller than average.² Taller people could be smarter and higher-earning because of something to do with those bigger brains they have, or they could have been able to get taller because they were more insulated from disease when they were growing up. Whatever the reasons, the relationship is there.

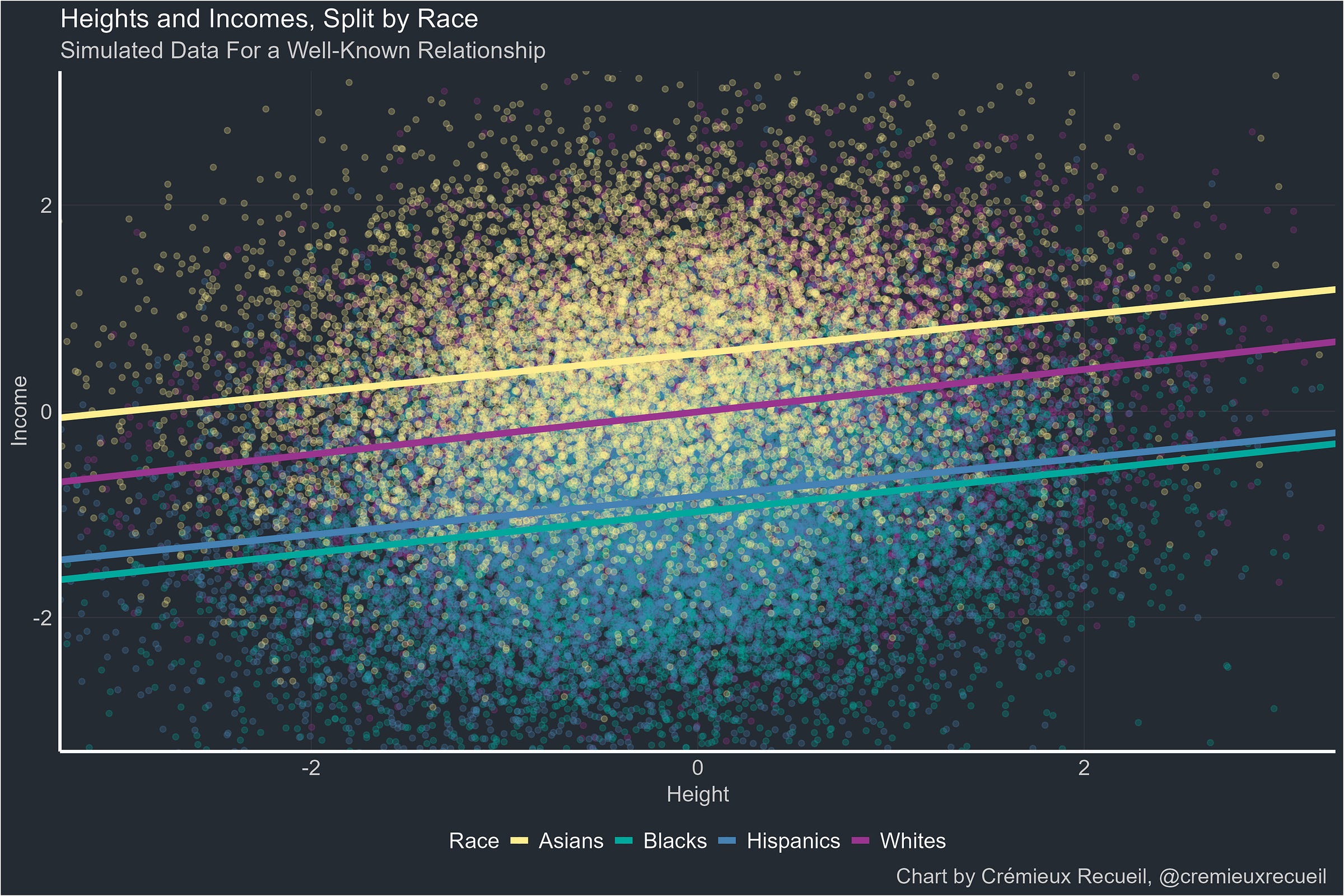
If we observed that height and income correlated at r = 0.2 and we only reasoned from the slope, we would predict that Asians and Hispanics should earn comparable, low amounts, that Blacks should earn slightly more than Asians and Hispanics, and that they should all earn less than Whites, on average. But in reality, we know this isn’t true: Asians tend to earn more than Whites, who tend to earn more than Hispanics, who tend to earn similar amounts to Blacks, whereas the height order is Whites > Blacks > Hispanics and Asians, resulting in a graph like so:

If we reverse the X- and Y-axes, we get a picture that looks even more confusing:

Similarly, the height and intelligence rank orders do not match up, since Asians > Whites > Hispanics > Blacks.

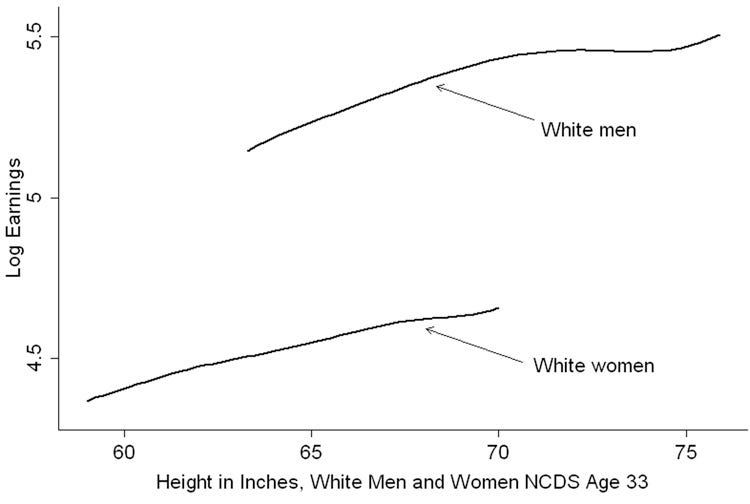
To bring this back to well-trod territory, think about height and income differences by sex. Everyone knows the ‘gender wage gap’ is affected by things like maternal duties, preferences for longer or shorter work hours, differences in occupational preferences, the confidence to ask for promotions, and so on. Men and women also vary in height. If we reasoned solely from the slope, then we would conclude that if women were—say—1.5 d shorter than men, then the income gap should only be 1.5 * 0.2 = 0.3 d. Moreover, an implication of slope-based reasoning is that if we stratified men and women by height, the income gap should disappear.

Well, does it? Alas:

Case and Paxson 2008, Figure 2

Clearly the incomes of men and women are not simply differentiated by heights, even if in both sexes, there is a positive height-by-income correlation. What we miss when we ignore intercepts in favor of reasoning from the slope is all other factors that independently explain gaps in the dependent variables.

So please: Don’t reason from slopes unless you also know about the intercepts, and if you absolutely must, at least try to ensure the slopes are the same across groups.

1. If this accrues no benefits—as seems to be the case—, it’s unclear why this should be called an advantage. It’s more like ‘the male brain size increment’.

2. In fact, higher-paid CEOs tend to be taller.