The Deep Roots of Intelligence Differences

Measuring differences in the past is a viable way to confirm present ones

Measuring Historical Cognitive Skills

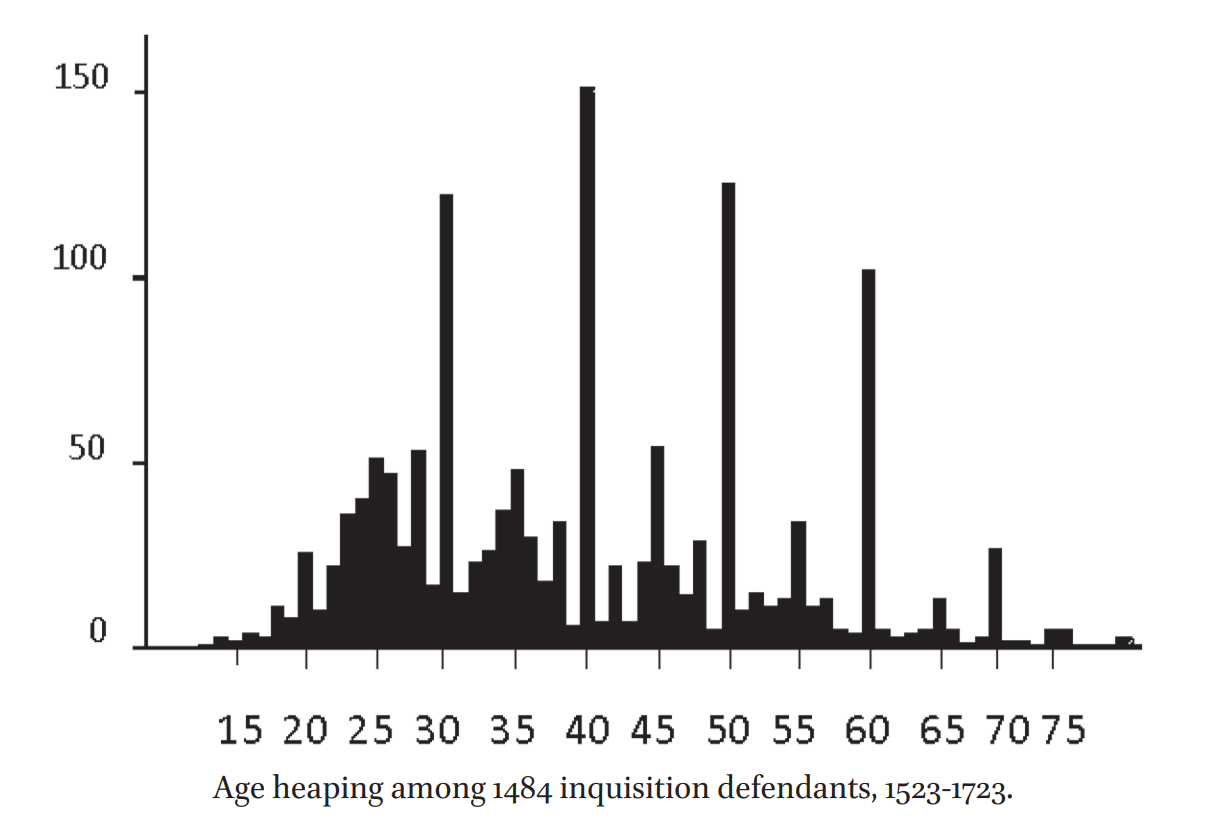
In 2009, A’Hearn, Baten & Crayen (henceforth, ABC) published a stunning paper in which they showed how to quantify historical numeracy through age heaping. To understand age heaping, consider these Neapolitan self-reported ages from the First Italian National Census:

The circled ages stand out: why are there so many people past their early years with ages at multiples of 10? Those are heaps: ages where there’s an excess of recorded people over the null expectation of a uniform distribution of terminals digits at intervals of 5, 10,¹ even numbers, or in some cultures, at numbers that hold a special significance, like 18 in Judaism or 8 in China.

The extent of age heaping is a good measure of numeracy for the simple reason that it indicates people aren’t good at subtracting their birth year from the current year. If it’s gathered from tombstones, marriage records, or reporting by different people, it might also indicate a culture of laxness around numbers. As ABC so eloquently put it:

[Just as the ability to sign one’s signature] can proxy for literacy, so accuracy of age reporting can proxy for numeracy, and for human capital more generally. A society in which individuals know their age only approximately is a society in which life is not governed by the calendar and the clock but by the seasonal cycle; in which birth dates are not recorded by families or authorities; in which few individuals must document their age in connection with privileges (voting, office-holding, marriage, holy orders) or obligations (military service, taxation); in which individuals who do know their birth year struggle to accurately calculate their age from the current year. Approximation in age awareness manifests itself in the phenomenon of “heaping” in self-reported age data. Individuals lacking certain knowledge of their age rarely state this openly, but choose instead a figure they deem plausible. They do not choose randomly, but have a systematic tendency to prefer “attractive” numbers, such as those ending in 5 or 0, even numbers, or—in some societies—numbers with other specific terminal digits.

This phenomenon is valuable for three main reasons.

Firstly, it is extraordinarily available.

Such “age heaping” can be assessed in a wide range of sources: census returns, tombstones, necrologies, muster lists, legal records, or tax data, for example. While care must be exercised in ascertaining possible biases, such data are much more widely available than signature rates and other proxies for human capital.

Secondly, its development precedes literacy. Large groups develop basic numerical skills prior to developing basic literate ones, and to some extent, numericity seems to be innate, whereas reading and writing skills are more culture-bound and not quite so easy to develop. Consider peasant Uzbeks, the Evenk, and the Altai, who were horrendously uneducated, but still had some appearance of basic numerical sense despite illiteracy and meager abstract reasoning skills. In a particularly revealing case, Alexander Luria recorded that illiterate Uzbeks could not complete syllogisms:

Illiterate Uzbeks peasants were unable to... solve syllogisms. For instance, given the syllogism “There are no camels in Germany; the city of B is in Germany; are there camels there?” Luria gave as a typical Uzbeks answer “I don't know, I have never seen German cities. If B is a large city, there should be camels there.” Similarly, Luria asked “In the far north, where there is snow, all bears are white; Novia Zemlya is in the far north; what color are the bears in Novia Zemlya?”. A typical Uzbek answer was “I've never been to the far north and never seen bears”.

Many non-human animals have been recorded learning numerically, and even fish seem to have a basic sense of numericity. Rudimentary numerical skills are much less likely to be biased due to differences in opportunity than are literacy skills. This is critically important when dealing with historical data, since changes in educational opportunities are often closely associated with or explicitly the topic being investigated.

And finally, these measures are validated. If you’ve seen a map of Italian statistics, it probably looked like this:

Well, here’s numeracy as calculated from age heaping (given by the Whipple Index) over thirty years of 19ᵗʰ-century Italian census data.

Not only that, but this measure of numeracy was related to Italian literacy rates and heights, and it has improved substantially from the 19ᵗʰ century into the 21ˢᵗ century as universal education has reduced the proportions of people who only sort of know their ages. But age heaping is still a problem in the developing world and, much more amusingly, despite mass education, age heaping hasn’t been eliminated in the developed world.²

We know schooling helps, so how much of the variance in age heaping is personal versus a reflection of the social level of schooling? ABC worked that out using the Integrated Public Use Microdata Series (IPUMS) collection of U.S. Census data from 1850, 1870, and 1900. They computed literacy and numeracy rates for 213 regions, defined as a combination of a birthplace, a Census year, and an ethnic group with at least 100 person observations. They then estimated the marginal effects of personal and regional literacy on the probability of reporting a heaped age across low- (mean heaping = 37.2%) and high-literacy regions (25.4%). This is what they found:

There was a notable interaction by regional literacy: personal literacy was significantly (p = 0.006) more strongly related to a reduced probability of providing a heaped age in regions where literacy rates were low; the effect of regional literacy did not vary (p ≈ 0.38). From this illustration, we know that the connection between literacy and numeracy is there and it can vary across regions.

In an impressive 2022 study, Baten, Benati & Ferber showed that 19ᵗʰ-century age heaping and literacy were linked in Italy for both men and women, albeit with a slightly weaker relationship for women. In the same study, they made the connection between age heaping and modern test performance explicit. For example, they took results from the West African Programme for the Analysis of Education Systems (PASEC) and showed that children’s measured numerical abilities were correlated with parental age heaping. At the region level within Burkina Faso, the correlation was 0.78, and in Niger, it was 0.95. For all countries in West and West-Central Africa who participated in PASEC, the correlation went up to 0.80. Within 114 African regions with mathematics test and age heaping results, the correlations ranged between 0.40 and 0.71, and these were all results from the 21ˢᵗ century. In Chad, Togo and Sierra Leone, this replicated again with 20ᵗʰ and 21ˢᵗ-century data, even when controls for family wealth and regional numeracy were included.

Baten & Juif extended the literature on test scores in 2014 by correlating international differences in age heaping-based numeracy across countries in 1820 with performance on mathematics and science tests between 1960 and 2000 and finding that, again, the correlation was very strong. Francis & Kirkegaard replicated this finding even more recently in the latter half of 2022. They found that 19ᵗʰ-century age heaping was a good instrument for modern-day national IQs and it predicted modern economic growth rates. In another study from 2022, Kirkegaard & Piffer found that performance on Italian standardized tests was strongly related to age heaping in 1861, 1871, and 1881; in another study from the same year, Piffer & Lynn found that those test score differences were related to regional differences in educational attainment polygenic scores.

In what I believe to be the most bizarre study in this entire line of work, Baten & Nalle extended the age heaping literature while also helping to prove the strength of the positive manifold of intelligence. To do this, they used data from interrogations by the Spanish Inquisition.

Inquisitors would ask people for their ages and then force them to provide a detailed reconstruction of their life narrative up to that point. Inquisitors, being intelligent men, were able to use these life course reconstructions to figure out if someone was lying based on slip-ups in their stories. For example, if a man recounted that he was 30 years old, married when he was 20, and then worked for 15 years on a farm, the inquisitor would be able to catch this mistake. People with heaped ages were 72% more likely to make a life course reckoning error, and this enhanced likelihood of error was robust to a variety of controls, including for occupation.

If you’re historically informed, you might know that many of the defendants in cases of inquisitorial interrogation were ethnic Jews. Across Europe, Jews were and have been very successful due, historically, to their unique occupational positions. Because Jews today are known to be quite smart, it has been speculated that this also helps to explain their positions in the past. Thanks to the Inquisition’s excellent record keeping, we know that Jews were smart during the reign of the Inquisition: the Sephardic Conversos and the more-often Ashkenazi Luso-Conversos both showed high literacy and numeracy relative to Spanish gentiles, but the Luso-Conversos—perhaps due to their trades—had even higher numeracy. In fact, said Sara Nalle:

So for literacy and numeracy—it is not necessary to pile on more evidence to prove that by whatever measure one picks, the Luso-conversos were exceptional compared to their Converso cousins, the general population of Old Christians, and the Moriscos.

When interrogated, it was Jews who best survived a bout with life course reckoning, and this performance was markedly better among the Luso-Conversos. Not only that, but Jewish reckoning was modern: it included dates and was not merely self-referential like the overwhelming majority of life course reckonings. To wit:

What seems so natural today was completely exceptional in the sixteenth and seventeenth centuries. Only 10% of the 247 Old Christian males used dates when giving their life history. Of those just a few could casually weave a narrative around the dates, rather than going from life event to life event. None of the Old Christian women in the sample—39 in all—used a year in their declarations whereas seven of the fifty Luso-conversas incorporated dates in their narrative. So, to answer the question, “Were any of the men and women in this study capable of that leap into a modern sensibility of oneself?”: the answer is yes, a very few, and they were Judeoconverso men. […]

By looking at how persons delivered the required discurso de la vida, some of the Luso-conversos, and to a lesser degree, the Castilian Conversos, proved that they had made the transition from a self-referential understanding of one’s life to one that showed an ability to situate oneself within the wider world of human activity. These findings by themselves do not prove the “modernity” of the Sephardic Jews and Conversos, but, when their well-established reputation for religious skepticism and other aspects of their collective identity are taken into account, there is no denying that the Judeoconverso minority exhibited in the seventeenth century most of the traits that we would associated with Jewish modernity.

From this discussion, we’ve gathered that there are at least two valid, widely available measures of premodern cognitive skills: poor rounding practices in age reporting, and the ability to sign your signature.³ They are measures of conceptually independent skills and they’re clearly correlated with one another, both in the past and in the present day. They also vary with intra- and international differences in literacy and development, and, as reported by ABC and subsequent papers that spawned from theirs, these measures have done so for centuries. These two measures are good—if crude—indices of cognitive ability—or in other words, they’re measures of what we’ve come to know as intelligence.

---

Putting Heaps and Signatures to Use

People have wondered for a long time to what extent gaps in cognitive performance between groups are stable and how much they might have changed. We know that the Black-White intelligence gap in the U.S. sits at around 1 standard deviation in size today. But has it always been this way? There’s no way to know for sure, but ABC gave us one interesting tell: they computed literacy and numeracy rates for Whites and Blacks from Census data gathered in 1850, 1870, and 1900.

The quantities they estimated might not produce valid results today because of range restriction, but this wasn’t true in the 19ᵗʰ century. Being totally or practically uneducated was much more common back then. Because it was and remains more common among Blacks than Whites, these measures will underestimate differences when Whites are near 100% literacy or numeracy, but let’s just see how they look.

One immediately apparent aspect of these data is that Blacks stagnated or worsened in these measures between 1850 and 1870. That’s due to the simple fact that the 1850 Blacks were freedmen and the 1870s Blacks were also free, but they included numerous people who were recently freed from slavery and were thus more poorly educated.⁴ Heaping also tends to happen more at later ages,⁵ so slaves ought to have had less of it due to their relatively young age structure. Nevertheless, we see a return to trend by the 1900 Census consistent with the fact that, as I’ve noted before, the effects of slavery quickly disappeared.

While these numbers are fine and dandy as they’re presented, they’re not really the terms people are familiar with when it comes to group comparisons.

If we assume literacy and numeracy are normally distributed and the group’s variances are equal, we can straightforwardly compute the gaps in standard deviation terms. To obtain a composite cognitive ability gap, we need to know how correlated these two quantities are,⁶ but those numbers weren’t explicitly reported in the paper. However, ABC did leave us some hints. For example, In Table 1, there’s a row of OLS regression slopes, showing that the region-level R² for the whole sample was 0.68. We can also see that this R² was 0.88 for Whites in 1850 versus 0.69 for Blacks in the same year. In 1870, these values converged: 0.69 for Whites and 0.72 for Blacks. By 1900, the slope had shrunken considerably to a mere 0.36 for Whites, but it increased to 0.82 for Blacks. A likely explanation for at least part of this observed instability, variance in the regional differences, and part of the group differences, is range restriction.⁷

Since ABC didn’t report the correlations we need—which may have been in their now-missing appendix—we can just simulate what the gaps would be at different levels of correlation. We’ll do this with gaps based on the observed ones, but we’ll also do two versions for the variances: one where they’re identical and one where the White variance is halved since Whites were always pushing against the limit.

Here’s how that looks:

The raw mean difference in 1850 was 0.754 SDs, and if we assume a correlation of 0.50 between literacy and numeracy, that increases to 0.796 SDs. If the White variance is constrained by half, that increases to 0.903 SDs. The raw mean difference in 1870 was 1.151 SDs, and a 0.50 correlation decreases that to 1.105, or 1.224 with constrained White variance. The raw mean difference in 1900 was 0.911 SDs, and a 0.50 correlation increases that to 0.929 SDs, or 1.044 with constrained White variance.

In other words, the 19ᵗʰ-century Black-White intelligence gap was highly similar to the one that has been regularly observed throughout the 20ᵗʰ and into the 21ˢᵗ century.

But this has been known for a while. The study this data came from was published in 2009 and Emil Kirkegaard noticed these gaps by 2017 at the latest. Whether this is really consistent with the modern Black-White gap is still dubious: we just don’t know if these tests were representative enough or if ABC’s definition of a “region” caused sampling problems, nor do we actually know if these results replicate beyond these three admittedly well-estimated datapoints.

Well, there are more datapoints out there. Let’s go through them.

First, and most relevant to American Black-White differences, Sohn provided data on numeracy gaps for Black and White Americans born in the 1820s, 1830s, and 1840s, as well as estimates for soldiers and non-soldiers born in the 1820s and 1830s, and many more Black and White soldiers assessed in 1880. Because knowing your age is important for soldiers but was less important for non-soldiers, there might be a bias in comparing those two groups. To that end, all of the comparisons I’m about to present are within the non-soldier and soldier groups.

79.5% of the Black soldiers born in the 1820s were numerate compared with 97% of the White soldiers from the same decade. For the soldiers born in the 1830s, 87.6% of Black soldiers were numerate compared with 99.2% of White soldiers. For the 1820s-born non-soldiers, 89.7% of Whites were numerate versus 57.4% of Blacks; for those born in the 1830s, the figures were 91.7% versus 59.2%; and for the 1840s, 87.5% and 64%. Sample sizes ranged between 931 (Black soldiers born in the 1820s) and 16,503 (White non-soldiers born in the 1830s).

These differences amounted to gaps of 1.057 SDs for soldiers in the 1820s and 1.254 SDs for the ones born in the 1830s. For the non-soldiers, the 1820s-, 1830s-, and 1840s-born gaps were 1.078, 1.152, and 0.792 SDs.

In the 1880s sample, being a soldier changed up everything. By that point, the 97.95% of White (n = 14,941) and 97.96% of Black (n = 1,225) soldiers were numerate. There was zero gap in age heaping between Black and White soldiers. It’s hard to explain the stunning homogeneity of these groups: did the military drill people’s ages and birth dates into their heads or did the military become extremely selective? Literacy information wasn’t included, so we can’t supplement our understanding in that way, and we don’t know anything else about how selective the military had become from this study either. Since we’re at an impasse, let’s look at the gaps between the immense (White n = 6,319,451; Black = 797,504) non-soldier samples. The gap between non-soldiers was 0.739 SDs.

To my knowledge, Sohn’s paper was the most recent foray into Black-White comparisons since ABC’s. But other group differences have been studied as well.

Juif & Baten compared age heaping practices between native Peruvians and their Spanish conquerors. They provided estimates of numeracy elative to non-migrant, rural, male, Peruvian Indios born between 1500 and 1549, ages 33–72, who had not been accused of being Jews. People whose records came from the Inquisition tended to be more numerate, and Jews were also more numerate above and beyond that. Women were less numerate, and urbanites were more numerate than people from rural areas. Juif & Baten documented that migrants tended to be more numerate than people who stayed where they were from, and then they presented additional national differences: Mulattos and Blacks were lumped together and they were less numerate; Indios in different places (Peru, Ecuador) tended to perform similarly to one another; people in Spain were more numerate, as were those in Portugal; Chileans, Bolivians, and Argentineans were migrated to Lima during their lives were also found to be more numerate. Numeracy non-monotonically trended up between 1450 and 1700 and with other data, they showed that was also true between 1350 and 1800 for other countries.

The scale of the White-Indio gaps was not the same as the White-Mulatto/Black gap. For example, the difference in 1650s Peru between Whites and Indios was 0.38 SDs, whereas the difference with Mulattos/Blacks was 1.05 SDs. At the same time, Spanish and Portuguese Whites outperformed the Whites born in Peru by 0.45 and 0.36 SDs, perhaps further supporting the place-contingency of basic numeracy and showing a possibly biased international comparison.

An even more recent publication by Pérez-Artés showed that Peninsulares who settled in Mexico had higher numeracy than those who settled in Peru. What’s more, migration was selective and it became less selective as the centuries went on.

Let’s go from bottom to top.

In the 16ᵗʰ century, migration to the Americas was extraordinarily selective: migrants were 1.638 SDs more numerate than stayers. By the 17ᵗʰ century, this gap had shrunken to 0.764 SDs, and by the 18ᵗʰ, it had fallen further to 0.438. It’s hard to tell what this gap really means, however, since the reason for the change was not so much a shift in the numeracy of migrants, but instead, in the numeracy of stayers. It seems quite likely that what happened was that non-migrants simply became less numerate for economic development reasons. If you compare migrants in the 16ᵗʰ century to those in the 18ᵗʰ, the gap is 0.117 SDs in favor of the earlier ones; but if you compare stayers in different centuries, the gap favors those in the 18ᵗʰ by 1.083 SDs.

Did migration really become less selective, or did skills in Spain rise? Or, alternatively, did the relationship between underlying numeracy and age heaping change? There’s indeterminacy, but we still wound up with two angles that suggested migration became less selective, and they should be biased in different ways: the gap between migrants and stayers could suggest indicator meaning drift, but the gap between migrants over time should consistently indicate human capital. So migration was selective, and quantifying the magnitude of it with respect to human capital and of changes in it over time is left as an exercise to the reader.

The differences between migrating Peninsulares who went to Mexico and Peru varied across the sixteenth century. In 1540, the Mexican migrants were ahead by 0.411 SDs, and by 1590, they were ahead by just 0.179 SDs; but in each decade, the ones headed to Mexico were ahead by some amount. This may go some way towards explaining why Mexico ended up being so much more productive than Peru.

Comparing said Mexican Peninsulares to the whole Mexican population, including Indios, Mestizos, Pardos, Criollos, etc., the migrant Peninsulares were ahead by 1.543 SDs in 1680 and 2.201 SDs in 1720.

Those last results are reminiscent of Calderón-Fernández, Dobado-González & García-Hiernaux’s results based on Mexican data from the 18ᵗʰ century.

They observed that in Oaxaca in 1777, Spaniards outperformed Mulattos by 0.445 SDs, while outperforming Mestizos by a smaller 0.341 SDs, and outperforming Indios by 0.571 SDs.

In Mexico City in 1790, the data was somewhat more detailed and it was available for a few different groups: Blacks, Castizos, Indios, Mestizos, and both Criollos and Peninsulares. Firstly, the Peninsulares outperformed by Criollos by a small margin, perhaps consistent with no real change in selectivity and some regression to the mean on the part of Criollos: 0.139 SDs. Combining these types of Spaniards, they outperformed Blacks by 0.399 SDs. More interestingly, they outperformed pureblooded Indios by 0.298 SDs, outperformed half-blooded Indios (Mestizos) by 0.171 SDs, and outperformed quarter-blooded Indios (Castizos) by 0.067 SDs (not significant).

Across an additional 24 Mexican localities circa 1790, we have data on Spaniards, Mulattos, Mestizos, and Castizos. The Spaniards outperformed Mulattos by 0.451 SDs, and outperformed Mestizos by 0.073 SDs, but across all these localities, Castizos actually managed to tie with the Spaniards, with only a 0.022 SD difference between them in the Castizo’s favor (not significant).⁸

To my knowledge, that exhausted the relevant group comparisons.

Or so I thought.

---

Admixture Effects: A Case of Deep Roots?

The burgeoning “Deep Roots” literature shows that people bring their culture-linked traits with them to the places they go. These culture-linked traits are also transmitted to people’s children, and this is still true when kids are adopted from an early age.

If you’d like an overview of the subject, it’s hard to recommend a better book than Garett Jones’ recently-released book The Culture Transplant.

There is a related literature on the subject of admixture. To understand admixture, consider a simple scenario: a man has a fully French father and a fully Polish mother. They have 50% French admixture and 50% Polish admixture. That person goes on to have kids with a woman who also has a fully French father and a fully Polish mother. Their kids will average 50% French and 50% Polish, but there will be deviations, since the parts of their parents’ DNA that they inherit are randomized due to recombination. Over many generations, this French-Polish population may be, say, 35% Polish and 65% French, with a standard deviation of 10%.

Now further suppose that the Polish are 5 centimeters taller than the French. For the sake of example, that’s 1.5 standard deviations! Naturally, we want to know why such a large gap happens.

Is it because the French and the Polish have different environments that allow the Polish to grow taller? That’s hard to know. Luckily, we know there’s a large sample of 35% Polish, 65% French people who can help us out.

If they’re all genotyped, we simply compute each individual’s Polish and French admixture in that sample and we compare them with a supposedly fully French and a supposedly fully Polish sample. Let’s say that there’s gene flow and the French sample was actually just 98.5% French, with a 1.5% Polish part and a standard deviation of 2% and the Polish are their inverse.

Since we have everyone’s French and Polish admixture calculated, let’s compare it to their heights. If we find that Polish admixture comes with greater heights, recall that the French and Polish samples are basically homogeneous. As a result, we might just be regressing between clusters where there’s no real relationship. So for greater inferential clarity, we should focus our results on the admixed and much more variable French-Polish population sample. If we know that they are 35% Polish with a standard deviation of 10% and the Polish sample is 98.5% Polish, then for genes to fully account for the difference between the French and Polish, the correlation between heights and Polish admixture in the mixed French-Polish group should be 1.5/(0.635/0.100) = 0.236. If we find a correlation of 0.20, then our result is consistent with 85% of the French-Polish difference being down to genetic differences between the French and Poles.

But further imagine that we live in a world where discrimination on the basis of French appearance is rampant and is capable of reducing someone’s stature. If French admixture merely tags French appearances and people receive quantitatively lesser discrimination if they have more a more Polish appearance, then the estimand might have to do with the effects of discrimination instead. We can make ourselves a bit more sure by including a covariate like French appearance ratings in our regression as a control. But we can also take a causal step and look within families.

As mentioned earlier, siblings with admixed parents vary in terms of admixture due to recombination. For causal inference purposes, this is a god-given natural experiment waiting to happen. All we have to do to understand whether the French-Polish difference is genetic without interference from traits that covary with admixture in the general population but not within families due to independent assortment and linkage, is to check if more Polish sibling pairs are taller.

Since this analysis requires enormous samples to be well-powered, it cannot be attempted without much larger samples than are presently available for many traits. The non-sibling design can still be highly informative, and it at least gives us a prior. If it supports a large percentage of group differences being attributable to admixture, then proposed non-genetic explanations will have to be based on there being some mediator that strongly covaries with admixture.

The non-sibling version of this design has been implemented for comparisons between Pygmies and neighboring non-Pygmy populations.

One of the recent triumphs of IQ researchers has been to find and replicate associations between admixture and intelligence, allowing them to clearly show genetic contributions to group differences in intelligence. Or, if you wish an alternative, it might be simply labeled contributions to group differences in intelligence that are strongly associated with genetic differences between groups.

The Deep Roots literature is connected with these admixture studies because genes are an obvious, powerful, and—importantly—reliable way to transmit traits whose effects we frequently associate with different cultures. Moreover, admixture also relates to identification with particular cultural groups.

Here are some recent examples:

• Bryc et al. (2015) found that the mean person’s self-identification as African American was nearly perfectly predictable from their genetic ancestry using data from 23andMe customers.

• Fang et al. (2019) showed a stunning concordance between self-identified race/ethnicity (“SIRE”) and genetic ancestry in the Million Veteran Program.

• Nagar, Conley & Jordan (2020) showed the same stunning concordance in the Health and Retirement Study.

• Kirkegaard (2021) used multinomial regression to predict social race from genetic ancestry and used Dirichlet regression to show their concordance in the Pediatric Imaging, Neurocognition, and Genetics dataset. These methods were used to estimate an AUC of 0.89 and an R² of 0.884. Since several of the groups in the dataset were small, and some of them were ancestrally very mixed (e.g., Hispanics), he also subset to Whites, Blacks, and biracial “Black-White” people and achieved an AUC of 0.994 and an R² of 0.951.

These and other recent analyses have produced results that smack you between the eyes because they should be obvious. And yet, these results are vehemently denied by people who should know better.

If you’re the visually-learning sort and you’d like to see how these studies tend to turn out, just take a look at Nagar, Conley & Jordan’s result:

Since admixture and self-identification are so closely intertwined, if traits vary with admixture, that means we can quantitatively investigate whether the cultural-linked traits of SIRE groups have a genetic component.

The design is simple, but it requires a lot of power for both the sibling and non-sibling versions. The latest studies have all had at least a thousand participants, they’ve all run with the non-sibling design, and they’ve all produced the same result: admixture statistically explains an enormous part of the intelligence differences between SIRE groups in the U.S.

Fuerst & Hu is the latest addition to this growing literature and it is also the first work of which I am aware that explicitly ties admixture studies to the Deep Roots literature.

The way they did this was clever.

First, they ran an admixture-intelligence study with the Adolescent Brain Cognitive Development cohort and they replicated recent results using that sample of around 11,000 9-to-10-year old children sampled between September 1ˢᵗ, 2016 and August 31ˢᵗ, 2018. They observed all the typical findings: a 1.10 Hedge’s g gap in intelligence between Blacks and Whites; Whites were 98% European and Blacks were 72% African; and admixture mediated 75.68% of the difference in intelligence between Blacks and Whites, as indicated by the 0.18 correlation within the Black group.⁹

The critical part of this analysis was that they created expectations: they documented how admixture was associated with measured intelligence in contemporary SIRE groups, who have obvious continuity with similarly-labeled groups in the past.

Second, they performed individual-level Census-based age heaping analyses and used mixed-race classifications to see if the time’s crudely-assessed admixture and crudely-assessed numeracy were related as one might expect given the modern data. This analysis relied on data from Censuses from 1850 to 1930.

If the two analyses are concordant, it suggests that the admixture-related gaps observed today are quite old and that they’re derived from common factors over an incredibly long time. If true, hypothetical explanations may need to be enormously constrained.

Finally, they did all of this beyond Black and White. Fuerst & Hu used Black and Mulatto slave samples in addition to samples of free Whites, Mulattos, and Blacks, they used Amerindian schedule samples and a sample of 5% of the country’s Amerindians, and they topped it all off by using samples of 12% of Puerto Ricans. These samples were very large, and they were able to go back and add cognitive ability assessments that the original enumerators never intended. If this wasn’t clever, it was at least a lot of work.

---

Admixture and Intelligence in the 21ˢᵗ Century

In the ABCD, the cognitive comparisons were unbiased. That means whatever the intelligence test they used measured was the same in different groups and it possesses the same causes. Because they used a valid intelligence test, they found evidence for racial differences in intelligence. But how large were those differences?

The White group was 98% European (σ = 0.05) with the remainder largely being African and East Asian. Amerindian contributions to White admixture were negligible. The Black group on the other hand, was 24% European (0.16), 3% East Asian (0.04), and 72% African (0.16), with a small Amerindian residual (<0.01, σ = 0.02). The Amerindian group was typical, which may sound unusual. It was 80% European (0.26), with 8% derivation from Africa (0.20), 3% from East Asia (0.08), and 9% from American Indians (0.15). The Puerto Rican group was 67% European (0.20), 8% Amerindian (0.07), 24% African (0.20), and 2% East Asian (0.03).

The study authors also computed information about the group’s skin tones. The White group had a mean Fitzpatrick score of 18.22 (σ = 4.96), meaning that they’re slightly tan but they’ll still burn. The Black group had a mean Fitzpatrick score of 33.31 (4.38), meaning that they were a dark brown and it would be really difficult to burn them. The Amerindian group had a mean Fitzpatrick score of 22.23 (7.20), so they’ll burn minimally and tan well. The Puerto Rican group had a mean Fitzpatrick score of 27.68 (6.64), so they’ll also minimally burn and readily tan.

This skin color information is important to know because “colorism”—discrimination on the basis of color—is the dominant proposed alternative for non-sibling admixture studies, because admixture and color are expected to covary. As a quick test of this, consider this table:

The higher the Fitzpatrick Type letter, the darker the person. In the two SIRE groups with sufficient variation in skin tone, darker people had less European admixture. Among Blacks, darker individuals also tended to be less intelligent. But among Puerto Ricans, that wasn’t true, although we shouldn’t think much of this since the result for the VI color category is likely unreliable due to its small sample size (n = 25).

In the White sample, there were minuscule relationships between ancestry or skin color and intelligence, ranging between ρ = -0.05 and 0.05, because the White group didn’t vary much in terms of admixture: they were pushing up on the border of being completely European. In the Black, Amerindian, and Puerto Rican groups—who are instead, characterized by a great deal of admixture—this wasn’t true and their results are more interesting.

In the Black sample, intelligence was correlated at 0.18 with European admixture and -0.20 with African admixture, in addition to negligible correlations of 0.06 with East Asian and -0.01 with Amerindian ancestry because those admixture types were limited in the Black sample. Fitzpatrick score correlated much more poorly with intelligence than European admixture did, at -0.09.

In the Amerindian sample, intelligence was correlated at 0.47 with European admixture and -0.18 with Amerindian admixture, along with correlations of -0.45 and -0.04 with African and East Asian admixture and a quite large -0.41 correlation with Fitzpatrick score.

In the Puerto Rican sample, intelligence was correlated at 0.21 with European admixture, -0.13 with Amerindian admixture, -0.17 with African admixture, and 0.02 with East Asian admixture. The correlation with Fitzpatrick score was 0.07, so darker Puerto Ricans were actually more intelligent in this sample. This should not be expected to replicate very well.

Now we have all of the information required to produce our expectations if 100% of the differences between these groups and Europeans are down to genes. Here’s a table that shows expectations with 100% genetic gaps versus what they observed in the study:

The results based on the correlations suggest that admixture explains the Black-White gap, but it’s worse at explaining the Amerindian-White or Puerto Rican-White gaps. One reason is variability: the Black group had more non-European range, and this was estimated better because they also had a much larger sample size. The second and more important reason is that the Amerindian and Puerto Rican groups have more complex admixture.

African American admixture is basically 1-African admixture, and the residual is overwhelmingly European and part of the assigned non-European admixture should probably not be considered Amerindian or East Asian but a fifth category: error. For the Amerindian groups, admixture is more complex. Their admixture didn’t arise from what was effectively a single event involving one other continental population. They’ve had long histories of mixing between multiple initially isolated populations, resulting in considerable percentages from different groups, and said admixture percentages don’t all have the same effects because different ancestral populations are varied.

So how much was actually mediated? Another non-sibling means of figuring this out is to enter the different ancestries into a regression simultaneously.

The first result worth noting was that for Blacks, Amerindians, and Puerto Ricans, skin color wasn’t a very powerful predictor. It wasn’t at all significant among Blacks or Amerindians, and it only had an unstandardized beta of 0.23 (p = 0.02) among the Puerto Rican sample. This compares with 0.03 and -0.01 in the Black sample. Since the significant Puerto Rican estimate was positive, it wasn’t consistent with standard Colorism theory anyway, since it meant darker Puerto Ricans performed better.¹⁰

The second noteworthy result was that African ancestry was a directionally consistent and significant predictor of poorer performance, and Amerindian ancestry was too, albeit not significantly in the Black or Amerindian groups.

The third noteworthy result was that after incorporating all of these different different ancestries, the Black-White difference was considerably shrunken, but it remained marginally significant (p = 0.02). The Amerindian-White and Puerto Rican-White differences, on the other hand, were no longer significant or considerable in size (p’s = 0.13 and 0.32).

To summarize these modern-day results, substantial parts of the intelligence differences between American Whites and several contemporary American population groups can be attributed to genetic differences. The way this effect manifests is in the form of greater intelligence among members of those populations who derive more of their ancestry from Europeans.

---

Admixture and Numeracy in the 19ᵗʰ and 20ᵗʰ Centuries

Section I: Blacks, Whites, and Mulattos

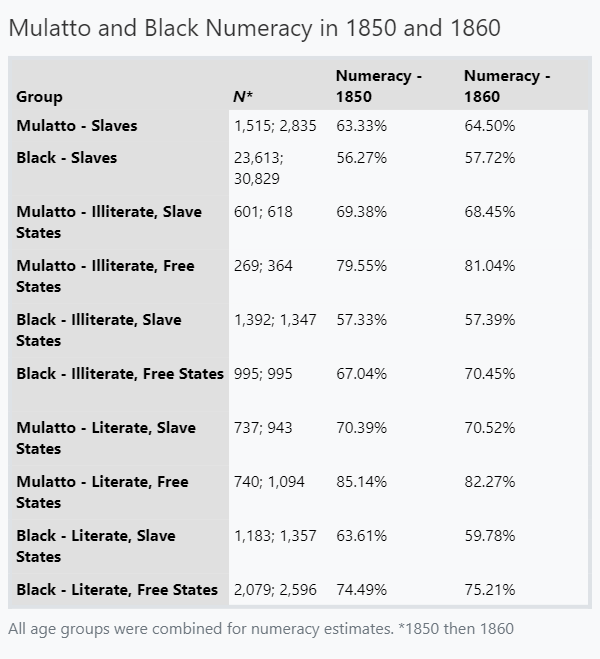
The best way to start this off is with an estimate that speaks to how environmentally contingent these results could be: a comparison of slaves. The groups being compared here are slaves deemed Black—which is to say, fully African—versus slaves deemed Mulatto—or half-White, half-Black. The samples these came from were representative samples of 5% of the slaves enumerated in the years 1850 and 1860. These samples were quite large and contained 1,515 Mulatto and 23,613 Black slaves in 1850 and 2,835 Mulatto and 30,829 Black slaves in 1860.

Now we’ll need a comparison group. Let’s use the Mulatto and Black groups in free samples from slave and non-slave states, who were literate and illiterate, respectively.

From the data, there was a 0.183 SD gap favoring Mulatto over Black slaves in 1850 and a 0.177 SD gap favoring them in 1860. This figure was again confirmed in the 1860 complete Census data, where a 0.169 SD difference between Mulatto and Black slaves was recorded with 7,660 Mulatto and 89,702 Black slaves.

The gap between literate Mulattos and literate Blacks in 1850 in slave states was 0.188 SDs, and by 1860, it had grown to 0.292 SDs. In the free states, the 1850 and 1860 literate Mulatto-Black gaps were 0.384 and 0.245 SDs. Perhaps sorting was involved in these changes, as the illiterate Mulatto-Black gaps in 1850 and 1860 in the slave states were 0.322 and 0.385, whereas in the free states, they were 0.294 and 0.342 SDs.

The table also shows that literate Mulattos in slave states performed more poorly than literate Blacks in free states. This isn’t quite unexpected. Comparing literate Mulattos in slave states to literate Blacks in free states in 1850 and 1860, the gaps were 0.123 SD and 0.142 SDs in favor of the Blacks. Comparing literate Whites in slave states to literate Whites in free states in 1850 and 1860, the gaps were 0.154 and 0.104 SDs. Add them up (0.265 SD gap vs 0.258) and they’re incredibly similar in size. Of course, this undersells the state effect: slave state Mulattos were beaten by 0.507 SDs by free state ones in 1850, and by 0.386 SDs in 1860; slave state Blacks were beaten by 0.310 SDs by free state ones in 1850, and by 0.433 SDs in 1860.

The state effects are impacted by selection, both on skills and ancestry. A crude corrective can be made based on the incorrect, but perhaps not strongly so, assumption that the White-White differences between slave and free states are due to the impacts of the states alone. So the corrected literate Mulatto-Mulatto and Black-Black gaps would be 0.353 (1850) and 0.282 (1860) SDs for Mulattos and 0.156 and 0.329 SDs for Blacks. The corrected Mulatto-Black gaps between these state pairs were 0.030 SDs in favor of Mulattos in 1850 and 0.038 SDs in favor of Blacks in 1860. In other words, the ancestry effect was enough to account for the state effects.

Was this so for the less-fortunate illiterate groups? Comparing illiterate Mulattos in slave and free states, the gap was 0.319 SDs in 1850 and 0.399 SDs in 1860. Comparing illiterate Blacks in those states, the gaps were 0.256 and 0.351 SDs. Comparing illiterate Mulattos in slave states to illiterate Blacks in free states, the illiterate Mulattos actually outperformed them by 0.066 SDs in 1850 and they fell behind by 0.057 SDs in 1860. Applying the correctives based on the White population from before, the illiterate slave-free Mulatto gaps dropped to 0.165 and 0.295 SDs, while the illiterate slave-free Black gaps dropped to 0.102 and 0.247 SDs, and the illiterate slave-free Mulatto-Black gaps increased to 0.22 SDs in favor of the Mulattos in slave states in 1850 and the 1860 estimate also changed directions to 0.047 SDs in favor of the Mulattos in slave states. The ancestry effect among the illiterate populations overpowered the state effects.

We still can’t be sure why these results were as they were since selection was at play in all of these statistics, and, for example, there may still be something akin to favoritism towards Mulattos over Blacks to different degrees in slave versus free states. However, we do have large-scale sibling comparisons from the time that tell us that appearance-based discrimination against Mulattos versus Blacks is not concerning, even if there appears to be a (genetically-confounded) relationship outside of the co-sibling control results. But regardless, to be more explicit, we need to increasingly incorporate Whites into these comparisons.

Firstly, the Mulatto-Black gaps for all freedmen in slave states, and all Mulattos and Blacks in free states in 1850 were 0.264 SDs, and 0.393 SDs in favor of Mulattos; in 1860, the gaps were 0.298 SDs and 0.274 SDs in favor of Mulattos. The Mulatto-Black gaps among slaves (0.183 and 0.177 SDs) were thus 69.32%, 59.40%, 46.56%, and 64.60% as large as these gaps, in those years. If we use the figures from the illiterate groups, the Mulatto-Black gaps were 56.83%, 45.97%, 62.24%, and 51.75% as large. Using the literate groups—which are arguably more comparable to the equality the Mulatto and Black groups in enslavement felt, compared to the comparably mixed illiterate group—97.34%, 60.62%, 47.66%, and 72.24% as large. Roughly half to two-thirds of the gap was preserved in slavery. We have suggestive evidence that the naïve correction for the White-White differences between free and slave states is incorrect, since correcting the total free state Black-Mulatto gaps for it suggests the gaps for slaves were 94.33% and 131.11% as large. For literate groups only, those numbers would be 79.57% and 125.53%, whereas for illiterate groups only, they would be 130.71% and 74.37%. Of course, these are possible, but doubtful.

Next, if we estimate Black and Mulatto performance relative to Whites, we can obtain a crude estimate of the extent to which genetics play a role. All we have to assume is that in terms of admixture, Mulattos are exactly in-between Blacks and Whites. This is an incorrect assumption that will be affected by range restriction if there are very European Mulattos, of which we know there are several, and of course it is also dependent on sampling error. If we had genetic data, we could tune up the estimate by using the exact admixture levels of the samples. But since we do not, we’ll have to proceed armed with our assumption. To use it, we simply take the performance midpoint for Blacks and Whites and compare it to how Mulattos perform.

Using samples including literate and illiterate persons, in the slave states, Mulattos performed 0.687 SDs worse than Whites, and Blacks performed 0.943 SDs worse than them in 1850. The Black-White midpoint is 0.472 SDs. Mulattos performed a bit worse than expected, so the estimated genetic contribution is 54.29%. In the same year, the gap in free states was 0.422 SDs and 0.815 SDs, for a midpoint of 0.408 SDs and a possible genetic contribution of 96.44%! Well now we need to check the results from 1860. In the slave states, Mulattos performed 0.732 SDs worse than Whites, and Blacks performed 1.03 SDs worse. In the free states, Mulattos performed 0.473 SDs worse versus 0.747 SDs for Blacks. These state pairs had midpoints of 0.515 and 0.374, so genetics could explain 57.86% in slave states and 73.36% in free ones.

To index whether this was due to opportunity, we merely need to repeat the exercise with the purely literate and the illiterate samples.

For the literate, that meant 1850 slave state Black-White and Mulatto-White gaps of 0.906 and 0.718 SDs versus 0.749 and 0.365 SDs in free states, alongside 1860 Black-White and Mulatto-White gaps of 1.04 and 0.748 SDs in slave states, and 0.711 and 0.466 SDs in free ones. The scale of the differences between the literate and mixed literacy samples perhaps speaks to the true effect of literacy given its consistency. It also suggests that whatever effect it had was relatively comparable between races. So, in these times and places, our midpoints were 0.453, 0.375, 0.520, and 0.356 SDs, meaning that genetics could explain 41.50%, 97.46%, 56.15%, and 68.92% of the differences.

For the illiterate, that meant 1850 slave state Mulatto-White and Black-White gaps of 0.763 and 0.441 SDs versus 0.796 and 0.412 SDs in free states, alongside 1860 Black-White and Mulatto-White gaps of 0.825 and 0.531 SDs in slave states, and 0.691 and 0.349 SDs in free ones. In these times and places, our midpoints were 0.382, 0.375, 0.413, and 0.346 SDs, meaning that genetics could explain 84.40%, 96.48%, 71.27%, and 98.99% of the differences.

Genetics were consistently less capable of explaining the differences between between Blacks and Whites in slave states as compared to free ones, and in the condition of illiteracy for both Blacks and Whites, genetics seemed to matter more in both places, with regional equality in illiterate- and literate-group explanations in free states in the 1850s.

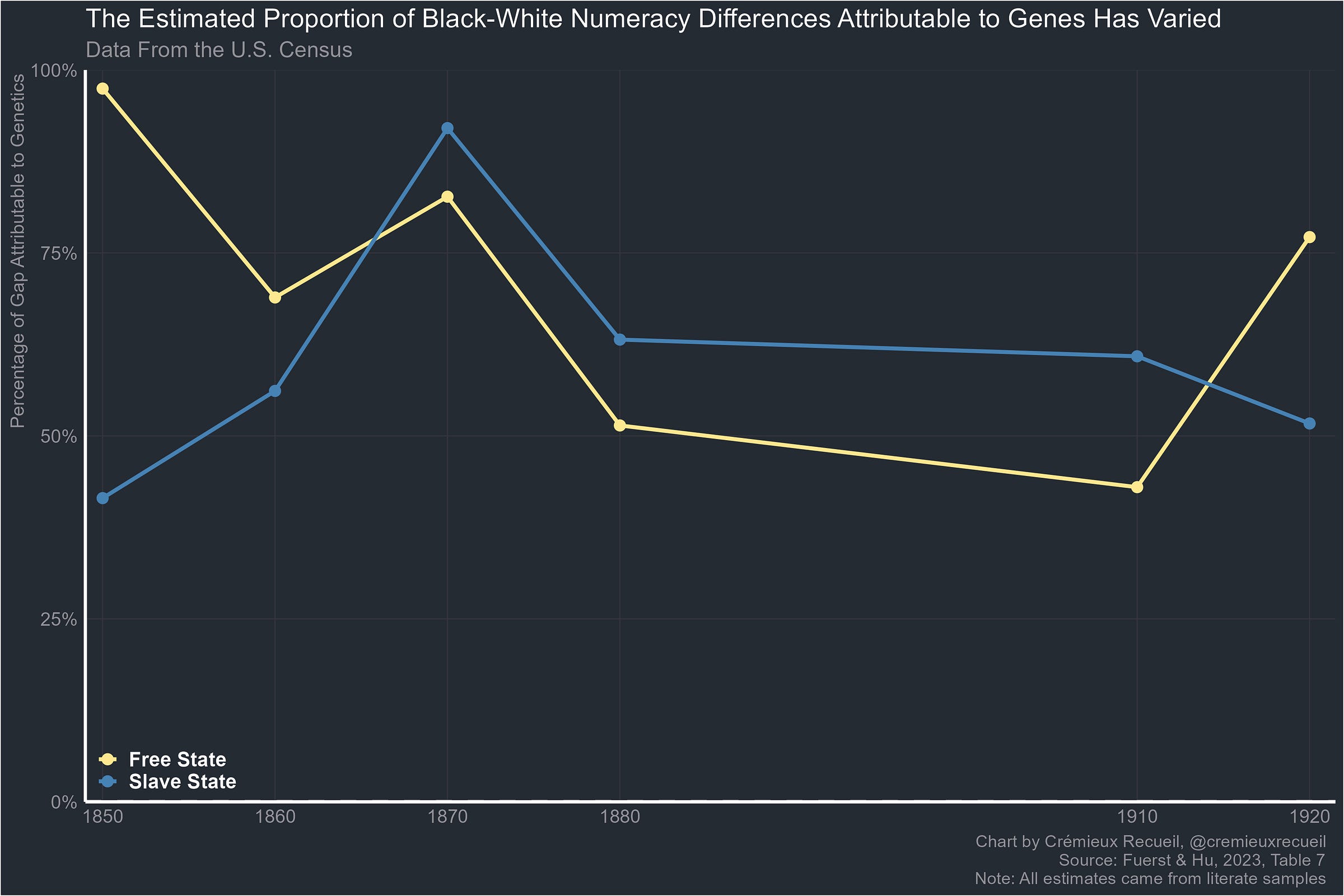
Now we really want to know why. So, why? Well, let’s inform ourselves by using data from 1870 to 1920. First step: check the consistency of the gaps. We know there was selective migration; we don’t know how that affected regional or temporal differences. Since literacy didn’t make a huge difference, we’ll also just use the literate samples.

And armed with our “Mulattos have the Black-White midpoint in terms of admixture” assumption, we can make another plot from this data:

These results are certainly something. They are directionally consistent with modern-day results, and they appear to be quite robust. There are directionally consistent differences among populations in slavery and out of slavery among the illiterate, among the literate, and across state lines and time. This is a single indicator of cognitive skills and it’s certainly not invariant—and due to the Black advantage in memory, it should favor that group somewhat—but it still manages to produce results that are consistent with those from the modern day. If we add in the literacy gaps, differences are probably biased up a bit (especially immediately after the Civil War), and we lose the ability to use literacy as an index of opportunity. Doing that doesn’t change the aggregate results all that much. That’s really something.

Section II: Whites and Amerindians

For this comparison, we’ll start with the data from two Amerindian schedule samples conducted in 1900 and 1910. These included literacy as a classification, and allowed the computation of numeracy for Amerindians who tribal elders reported as 0%, >0-25%, >25-50%, and >50% European, and White in 1910. Those individuals who were identified as fully-White were still listed as racially Amerindian.

Among the literate, this is how those two samples looked:

The results were consistent with illiterate samples, but there were simply too few people in the fully-White (n₁₉₀₀ = 0; n₁₉₁₀ = 29) and >50% European (n₁₉₀₀ = 54,; n₁₉₁₀ = 117) groups for those results to be worthwhile to present. However, there were thousands of completely Amerindian illiterates in 1900 (4,772) and 1910 (3,893), 167 >0% to 25% in 1900 and 185 in 1910, alongside 357 >25% to 50% in 1900 and 324 in 1910. If we use just those groups with decent sample sizes, the total 0% versus >25% to 50% gap in 1900 was 0.927 SDs and the literate-only gap was 0.614 SDs. In 1910, the total 0% versus >50% gap was 1.222 SDs and the literate-only gap was 1.166 SDs. For comparability, the 0% versus >25% to 50% gaps in 1910 were 0.918 and 0.731 SDs.

As the figure above shows, the development of numeracy gaps in this group of people who were all labeled Amerindian was continuous: more European admixture, higher numeracy. Contrarily, the moderately-sized fully-White-but-still-Amerindian sample included in 1910 was neck-and-neck with the Amerindians reported as >50% European in the same year. If we want, we can use their literacy rates to distinguish them. Doing that shows that the fully-White group outperformed the >50% European one by 0.218 SDs for averaged literacy and numeracy.

This doesn’t exhaust the Amerindian data. In the Censuses of 1900, 1910, and 1930, Amerindians outside of the schedule sample were coded up as either mixed-blooded or full-blooded and the overwhelming majority of that mixture was with Whites, so the admixture effect will primarily pertain to European admixture. Let’s go ahead and see how they looked:

In gap terms, in 1900, the gap between literate full-blooded Amerindians and literate mixed-blooded Amerindians was 0.769 SDs in favor of the mixed-blooded ones. In 1910, this gap developed to 0.861 SDs, and in 1930, it declined to 0.242 SDs. The illiterate groups produced gaps of 0.684, 0.666, and 0.086 in those years. In 1900 and 1910, the mixed-blooded illiterate group outperformed the full-blooded literate group by 0.081 SDs in 1900 and 0.031 SDs in 1910, but if fell behind by 1930, coming in at 0.199 SDs behind the literate full-blooded Amerindians.

This exhausts the Amerindian data. The results here showed that among Amerindians, that literate people were more numerate, and also, that less Amerindian ancestry came with greater numeracy.¹¹ As this group has basically fallen apart in more recent cohorts and most of the people who self-identify as Amerindian are now primarily ancestrally European, there’s obvious difficulty in treating estimates in different time periods comparably.

Who really knows what an Amerindian today is when he looks like a Swede? And how early did people start to self-identify with their Amerindian ancestry in this way? Until we know, interpretation here is limited. If we had indications that a person was Mestizo (i.e., half-Amerindian, half-White), then we could also compute the genetic contribution like we did with the Mulatto results.¹² But, these results still seem to be aligned with the modern ones.

Section III: Puerto Ricans

Puerto Rican Census results were available for the years 1910 and 1920. In Puerto Rico, racial identification differed: the categories meant different things than they did in America proper. A person might say they’re White, but they’ll really be, say, 50% Amerindian; they may say they’re Black, but they’re actually Mulatto. In general, a Puerto Rican person who identifies as White, Black, or Mulatto is actually nowhere near 100% European, 100% African, 50% of either or whatever their midpoint is for the social groups in that society. This misidentification relative to American identification was and remains so common, that it makes Puerto Rico a tidbit, more than something to substantively rely on.

However, we do have one comparison with categorical consistency that we can use to anchor the results: there were Whites from the U.S. who settled in Puerto Rico and were included in the island’s Census. These immigrants should be expected to be like other American Whites, i.e., around 100% European.

In 1910, 32.00%, 23.10%, and 27.05% of the Puerto Rican White, Mulatto, and Black samples were literate, respectively. In 1920, these figures were 39.11%, 31.72%, and 34.31%. In all of these cases, the U.S. Whites were literate. Because they immigrated to Puerto Rico, it might also be reasonable to insist they were selected with respect to numeracy, too. We can assess their numeracy relative to Whites in the other Census years in the mainland, so before relying on them to anchor our results, let’s do that.

U.S. Whites in Puerto Rico, as it turns out, were not selected relative to literate Whites in the U.S. proper. In 1910, the gap favored the Puerto Rico-based U.S. Whites by 0.118 SDs, and in 1920, it favored the U.S.-based Whites by 0.081 SDs. This is effectively no gap. We can safely use these U.S. Whites in Puerto Rico as an anchor, compared with the literate Puerto Rican groups. Let’s check how things looked:

In Puerto Rico, numeracy really didn’t seem to be racial. Instead, it was about literacy. The racial categories used in Puerto Rico probably just didn’t mean much with respect to ancestry. This seems likely because a U.S.-representative sample of Whites outperformed all of those groups’ literate members by 1.035 to 1.091 SDs in 1910 and 0.826 to 0.899 SDs in 1920.

It is unclear if this Puerto Rican data reconstituted the modern results because racial self-identifications seem to be a poor proxy for one specific type of ancestry in Puerto Rico compared to the U.S. These results still showed that a group we know to be almost-entirely European outperformed groups that we know to be variously mixed, but it didn’t provide us any quantitative indication of the differences. Then again, we don’t know if it should. Recall that in the modern results, there was a non-monotonic relationship between skin tone and intelligence, and, likely because of the different effects of different admixture sources on skin tone and intelligence, that non-monotonic relationship was also accompanied with monotonically decreasing European admixture.

Populations with more complex admixture histories will require deeper investigation; they may only be capable of being investigated with modern genomic methods.

---

Is Admixture a Source for Deep Roots?

Or in other words, do the modern and the mid-to-late-19ᵗʰ- and early-20ᵗʰ-century results align?

• For Black-White differences within the U.S.—Yes.

• For Amerindian-White differences within the U.S.—Yes.

• For Puerto Rican-White differences within the U.S. and in Puerto Rico—Maybe.

Admixture-related differences in intelligence, numeracy, literacy, cognitive performance—pick your fighter—are old. They are so old, in fact, that they were observed to comparable degrees not only throughout the 20ᵗʰ century, but in the 19ᵗʰ as well. The evidence presented here is consistent with there being deep roots for today’s admixture-related differences in intelligence.

One could claim modern results are biased. In that case, they’re wrong. One could claim the results using age heaping and literacy were biased in the past. In that case, they’re probably right, but the results still line up with today’s so closely that it’s hard to actually take this complaint seriously. It seems likely that, for as long as they’ve been recorded, group differences have been similarly-sized to those observed today, and that they varied accordingly with admixture and not appearance.

This post was merely descriptive. The dispositive high-powered co-sibling control—or ideally, co-dizygotic twin—test remains to be completed. We can only be sure that these results are well-aligned with genetics driving group differences in intelligence, and doing so consistently enough that any alternative theory will be forced to make wildly speculative and empirically dubious claims in opposition to it.

If, one day, someone linked together a dataset with these measures and a cognitive test, explicitly linking these measures to measured intelligence and measurement invariance could be tested. If measurement invariance held, it would further constrain explanations in the past like they’re constrained now. This constraint is very strong: whatever people wish to contend about modern results, their alternative hypotheses need to be about things that vary within the populations being analyzed, without suggesting that the differences are due to factors that only operate between groups.

Future analyses might feature groups like Asians and Ashkenazi Jews, who both outperform Whites. If, one day, there were samples of mixed-race Asian-White or Jewish-White samples to play around with, we might be able to see if there are benefits to certain types of non-European admixture among Whites, too. An additional possibility is performing these analyses with Sephardim and Ashkenazim, since it’s plausible a priori that the differences between them in a country like Israel would not be driven by discrimination.

Only time will tell if what the past reveals, the present shows, and the future holds are in agreement.¹³

1. This is presumably linked to the fact that people develop a preference for fives or tens since they first count on their hands.

2. This also reflects ‘other-sampling’ effects, where people approximately report the ages of people they’re asked about even though they might not misreport their own age.

3. Or performance on a simple literacy test.

4. The stagnation in age heaping rather than a decline in performance also speaks to its relative lack of bias with respect to opportunity.

5. This may be a source of error, so Crayen & Baten proposed a means of adjusting for it and if a paper provided adjusted estimates, I opted to use those instead of unadjusted ones.

6. I described why in a previous piece.

7. But crucially, not much: remember, differences near thresholds translate to larger standardized differences than those further away, and differences further from means have much larger representation differences than equivalently-sized ones nearer to means.

Two examples will suffice for clarification.

The first is for an index that’s bounded between 0 and 100%. A difference of 0.92 d if a high-scoring group is at 99% on this index would mean that the other group is at 92.02%. If the first group were instead at 90.41%, the second would be at 65% and there would still be a 0.92 d difference.

The second is for an index score with a mean of 100 and a standard deviation of 15, i.e., the typical “IQ-metric”. A score of 67 and a score of 70 have percentile ranks of 1.390 and 2.275. As a result, a score of 70 is 1.64 times as common as a score of 67. Scores of 95 and 98 have percentile ranks of 36.94 and 44.70. Accordingly, a score of 98 is only 1.21 times as common as a score of 95.

8. This study also showed that age heaping in 1820 predicted GDP in 1870 in a cross-national sample.

9. This proportion is 89.52% if you use their alternative g measure based on an MGCFA instead of the EFA-based one and you use their provided 0.18 European admixture-g correlation. The MGCFA-based gap was 0.93 g in size and the 0.18 correlation was not based on the MGCFA result, so it may be higher or lower with it, making this result indeterminate.

10. Thus making this result inconsistent with two of the studies on skin color and IQs in Puerto Rico cited by Fuerst & Hu: Vincenty (1930) and Green (1972).

11. Thus replicating Thornton & Young-DeMarco’s results for literacy.

12. For the sake of completeness, we could try something like this with the 1910 sample that included fully-White people: we could consider them 100% European and consider the 0% group exactly that, then treat a combined >0% to 25%, >25% to 50%, and >50% group as if it were a Mestizo group. Since only 29 of the fully-White group (6.50%) were illiterate, but far higher percentages of the other groups were, we should constrain this exercise to the literate samples. This leads to a midpoint of 0.561 and an amount explained by genetics equal to 46.52%.

13. Incidentally, Steve Sailer has just written an article on the subject of old studies of admixture differences.