The Status of the Shared Environment
A brief commentary on a recent post by Inquisitive Bird
Inquisitive Bird (IB) has a new piece correcting a common misconception about behavior genetic results: that they show parents “don’t matter.”
The article starts off by noting three common misinterpretations about behavior genetic results.
The first is that “small” proportions of the variance in a trait being explained by the shared environment, C, mean that C is unimportant and, consequently, can be dismissed. I think there are easy ways to explain this misconception. Consider, for example, what happens to the mean of a typical IQ distribution when the bottom 5, 10, and 20% of the variance (not the total sample) are removed. Using rnorm() and setting the seed to 1 with a million-observation sample size, the new means are 100.3, 100.7, and 101.8. But that also means dropping everyone with IQs below 63.5, 68.9, and 75.9.1 Using Danish administrative data, we can get a glimpse at the social impacts that could have:
The social impacts of doing this would be very considerable, and we also see something like this with crime data.
There are many other ways to show that small effects can matter a lot, like Abelson’s Paradox, <40% effective malaria vaccines that have nevertheless saved tons of lives, or that a minuscule 0.16 correlation between hours of social media use and depression can explain all of the recent rise in depression.2 Scott Alexander has more examples.
What seem to be small levels of C clearly cannot be dismissed out of hand for no other reason than that they feel small. The second point makes that even clearer; it is that effects are often compared in standardized terms while a proper comparison requires using unstandardized terms to understand different variance components in terms of their effects. Understanding this explains how, if additive genetic effects—A in the classical twin design—explain 80% of the variance in a trait, they’re only twice—rather than four times—as important for the trait as environments are. If genes were really four times as important as environments, genes would explain 80% of the variance versus 5% for environments. This puts effects in much more intuitive terms for understanding for the same reason. After all, 0.80 versus 0.20 is much less similar than 0.8944 versus 0.4472.
The final point was one that I also noted in an earlier article in Aporia: that low power often results in non-zero values of C being constrained to zero, leading to the incorrect conclusion that C really does equal zero.
The rest of IB’s article was a review of the best evidence for C on several social traits and the conclusion that for education, income, crime, and wealth, A > C by 1.4-2.1, 1.7-2.3, 2, and 1.3 times, respectively. Additionally, though genetics was more important throughout than the shared environment was, the nonshared environment—factors that make siblings neither more nor less similar to one another—was often the most important individual factor. This was not true for education or crime, but it was true for three of four income estimates and for wealth. So beyond the systematic factors (A and C), randomness and environments that siblings differentially respond to matter as well.
IB was careful to use estimates where assortative mating was accounted for, like adoption studies or adjusted twin studies. This is important, since many claims that C is sizable in the literature are down to little more than assortative mating creating the appearance of C, when it’s really small or absent. This problem gets down to the issue of what C actually is. A related, fourth issue I would have liked to see IB note is that C is not necessarily “nurture.”
In the standard twin model, C is, in theory, simply all factors beyond genes acting additively which make siblings appear more similar to one another. But theory falls apart when what we’re calling C can be dominance, D, or the result of assortative mating. Moreover, just because it’s factors that make siblings more similar to one another does not mean it’s factors that make family members more similar to one another. C is not necessarily the result of vertical transmission from parents or anything particular to a family as opposed to simply the sibling environment. Sometimes C isn’t even something shared by siblings per se, but instead, just by twins.3 Wolfram and Morris provided an example of that for educational attainment:
C might not even mean the same things across ages. For example, for the trait height, the C that’s present in childhood is probably something that actually has to do with the family environment, whereas in adulthood, if it remains at all, it probably has more to do with assortative mating. That’s just not something parents, families, siblings, twins, etc. have much control over.
This brings me to a fifth erroneous inference I would have liked to see IB note: that variance components defined in twin and family designs are not causal quantities. Due to their identification through god-given variation in relatedness, they are causal quantities. The only thing required to obtain causal identification with these models is that environments aren’t systematically more similar for more genetically similar individuals in a way that causally impacts traits to a meaningful degree. As Footnote 2 notes, this assumption tends to hold. Since this is so, it explains why there’s still “missing heritability”—at present, we cannot explain why twin and family estimates of heritabilities diverge from SNP heritabilities.4 We probably won’t have the required data to resolve the discrepancy for a while, but it’s likely that major parts of the difference are down to rare variants.
With these concerns out of the way, I want to delve into some unresolved and resolved or practically resolved issues that have to do with the shared environment and other estimates in typical twin and family models.
Behavior Genetic Methods Agree With Econometric and Epidemiological Ones
One potential topic of interest is whether causal estimates of environmental effects obtained from designs like adoption studies agree with the results of behavior genetic variance decompositions. This can be hard to quantify for two main reasons.
Firstly, because seemingly large effects are compatible with even very high heritability estimates. Jensen famously explained this fact in Let’s Understand Skodak and Skeels, Finally. He noted that the large IQ adoption gains observed in Skodak and Skeels’ adoption data were not inconsistent with a high heritability of 70-80%. Similarly, height is highly heritable within a given cohort, and yet it has majorly increased in the last century.5
Secondly, because different things are often being estimated with different designs, these different designs frequently come to different conclusions for artefactual reasons. Users of behavior genetic models often grasp the concepts of latent variables and their importance so, all else equal, you should expect them to be more likely than, say, econometricians, to model something like latent general intelligence, g, as opposed to modeling IQ scores. This can be very important, because things like adoption gains to IQ scores might be due to non-g factors, potentially limiting their importance and making the gains interpretable in a different way than the differences that exist between groups cross-sectionally.6 A related issue is when some treatment effect is a result of psychometric bias, as in the case of treatment effects on test scores that have their impacts solely through making people better at taking tests rather than improving the abilities that usually undergird test performance. It’s critical to understand this when interventions raise one group’s scores and not another’s and the groups could initially be compared in an unbiased way, as that implies the post-intervention comparison became biased.7
There are not many empirical examples where econometric or epidemiological estimates are put head to head with the ones you can obtain from behavior genetic models, but what few there are tend to agree with one another closely. A notable example comes from Sacerdote’s study of Korean adoptees, who are uniquely excellent samples adoptive samples since parents had no choice about which Korean adoptees they received, eliminating placement concerns and potentially explaining why there’s no relationship between age at placement and intelligence among Korean adoptees.
In Sacerdote’s study, he found that the estimated effect of being assigned to a highly educated and small family8 was a substantial increase in educational attainment, in the form of completing more years of education, being more likely to graduate any college, and being more likely to graduate from a selective college (“Adoption Treatment Effect”). The effect of moving up one standard deviation in assigned family C quality was very similar (“Variance Decomposition Effect”). See?
The latter effect was consistently greater than but similar in magnitude to the adoption treatment effect. This is likely because the adoption treatment effect proxied environmental quality to a more or less acceptable degree and the variance decomposition effect got it on the money because it was estimated at the latent level and it comprehensively indexed environmental qualities that make siblings more similar to one another instead of parental socioeconomic status alone. Behavior genetic estimates were probably consistent with a larger environmental effect because they constituted superior measures of the breadth of the environment.
This speaks to a few things. First of all, it speaks to how well these models work. Secondly, it speaks to the identity of C in this adoption scenario: it clearly seems to be indexing family environmental quality, not something specific to siblings per se.9 That’s good! Finally, it speaks to how much we could gain by appreciating how behavior genetic models can be used.
One perspective on behavior genetic models that follows from this is that they constitute great ways to quickly obtain treatment effects. Since the causal identification of arbitrarily defined variance components for all sorts of things is possible with more degrees of relatedness in the sample, practitioners can take these pretty far. For example, if your data has cousins, you can even readily ensure the “C” is defined the same way as it is in adoption studies, even if you don’t have adoptees in your sample. The utility of these models for causal inference has barely been scratched, and I assume part of the reason why is that their results are viewed in a poor light since they reveal how large the effects of genetics are, even if they also tell us about the effects of environments. These models are just viewed poorly by association and extended implication.
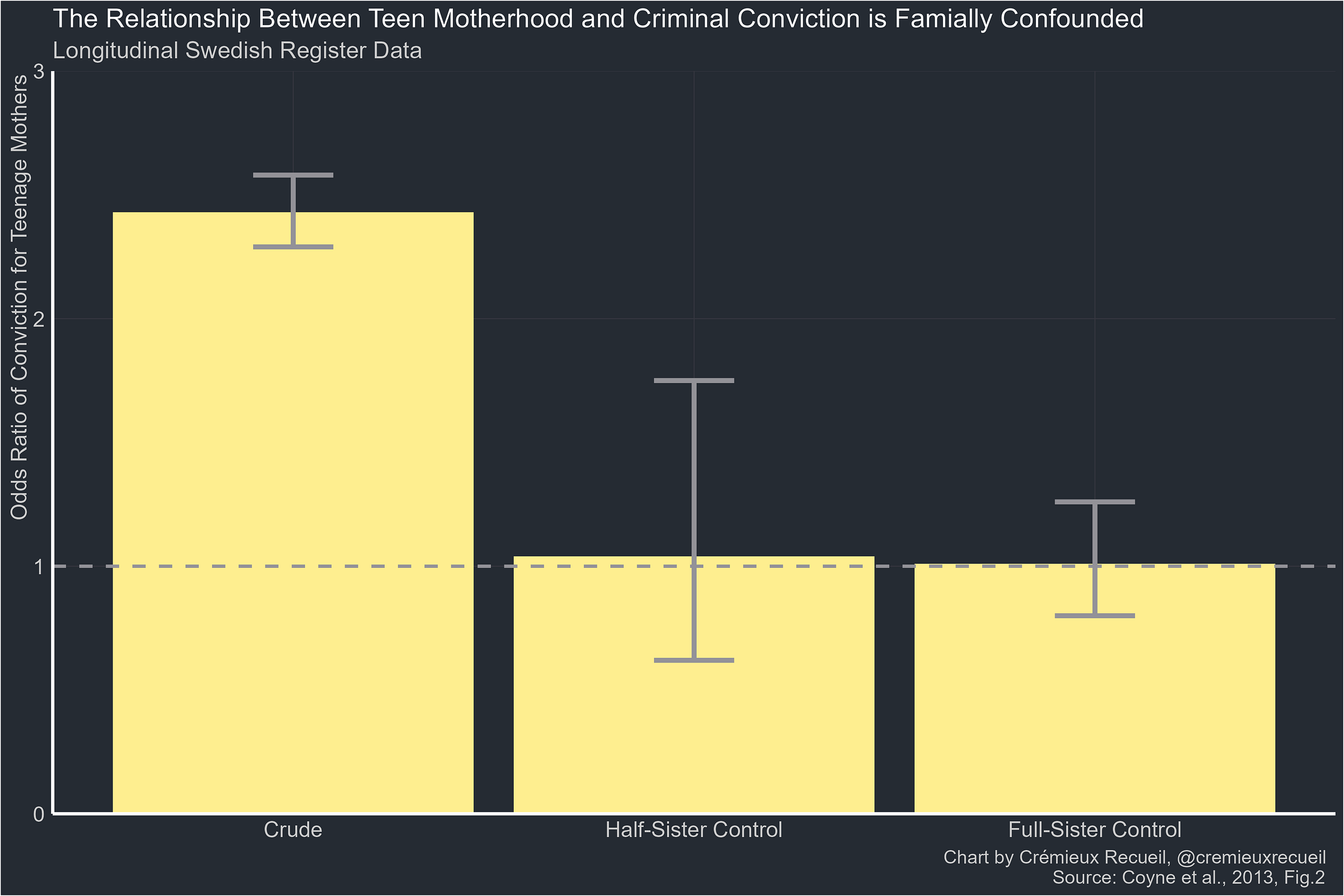
In an earlier article, I pointed out how the results of twin, sibling, cousin, and so on control models are predictable from behavior genetic decompositions, like the ACE model. One of my examples was how we knew that the relationship between being a teen mother and being convicted was due to shared environmental factors, so the half-sibling and sibling controls returned the same results. Other familial control results often return results showing greater moderation with increased genetic relatedness which is, predictably, the case for more heritable phenotypes.
This sort of finding gives us a lot of information. For one, it tells us that there’s value in twin and family behavior genetic models since they predict other results in intuitive ways. They are causal models, so of course they are tied to other causal methods whose estimands are linked to theirs. That is part of why we can often just substitute a twin model result for the direct assessment of whether a relationship holds up within some level of kinship—a consequence of the two things being directly linked. For two, this allows us to see how often twin and family model results agree with co-kin control results. Since I’ve only seen agreement so far (and if you’ve followed me, you’ll know I’ve seen hundreds of examples), I’m inclined to think this holds up in general, unless the twin/family model suffers from a serious bias specific to some phenotype or class of related phenotypes.
Because these models work to predict the results of other models,10 the case that missing heritability is a real problem we can’t sweep away is strengthened. Even still, we need more testing and more attempts to explicitly connect models; the validation process never ends, and if there are exceptions where models fail to predict results they should, we could gain valuable knowledge by understanding them.
Methods Agree: Interactions Are Still Rare
People often want gene-environment interactions to explain why C tends to be relatively small. They’ll say things like ‘the A factor is actually an gene-environment interactive AxC factor, not a pure A factor.’
No one has been able to find evidence for this sort of thing at scale, and we have both methods and ample data to find out if it’s true, so it should be considered surprising that people would make this sort of claim if they have a shred of honesty to them.
If you’re just working with twins, you might not be able to analytically identify an AxC factor. But that’s no problem, because the moments of the factor scores from your twin model will reveal evidence for variance in those factors being interactive if you’re well-powered to detect such effects. If you do have more than just twins, the analytic identification of interactive factors is possible. The model for this is simply
So here we have two methods for identifying whether there’s interactive variance in our variance decomposition. We can apply these methods to the Children of the National Longitudinal Survey of Youth’s data with the NlsyLinks R package and the supplied mathematics scores (MathStandardized) and height (HeightZGenderAge) variables, because I am being lazy and they’re precomputed. Doing this returns… no evidence of interactions with either factor scores or explicitly modeling AxC. If anyone would like to try this with other phenotypes, I’m all ears, but standing variance components are virtually never found to be interactive, so it would be a pretty neat finding if that weren’t the case.
This is effectively the conclusion reached by Hill, Goddard and Visscher, who investigated whether there was evidence for epistasis and dominance in different human traits and ended up finding that “interactions at the level of genes are not likely to generate much interaction at the level of variance.”11 The same is likely to be true for gene-environment interactions: even if some exist, in general, interactions supply little standing variance to traits.
Another method to test for gene-environment interactions is to leverage adoption data. Halpern-Manners et al. did this in 2020. They had data on biological and adoptive parents’ educational attainment and they were able to regress these attainments on three Woodcock-Johnson scores for adoptees. They found that adoptive effects were not driven down by range restriction, that post-natal contact wasn’t a moderator of adoptive or biological parent effects, and that adoptive and biological parent effects together seemed to equal the effects of biological parents in the non-adoptive, norming sample. Or in other words, the biological and environmental effects of parents were additive, not interactive.
The evidence that we need to worry about interactive effects is poor. The evidence for specific interactions like the Scarr-Rowe effect is modest, highly contextualized, and inconsistent enough12 to be unconcerning outside of specific scenarios.
Bias Still Confuses People
There is a particular part of some adoption studies like Skodak and Skeels’ that confuses a lot of people: in adulthood, kids’ measured IQs only covary with their biological parents, but their mean scores are sometimes more similar to their adoptive parents. Because adoptive parents tend to be more accomplished than people who give up their kids, you can probably guess that this means the adopted kids do better than their biological parents. That’s gains coexisting with biological effects—maybe.
No one has shown that this is a meaningful finding in any setting and all results that appear like this are, accordingly, confusing. In the case of Skodak and Skeels, we know it’s not a meaningful finding, since the biological mothers were tested years apart from their biological children, leading to the Flynn effect inflating children’s scores relative to their biological parents’.13 Since biological effects tend to be related to g and non-biological effects are not, we should also see the lack of a covariance with adoptive parents for what it is: a sign of psychometric bias afoot because the components of the mean scores for the biological and adoptive parents are apparently not alike.
Inattention to psychometric concerns is fatal for generating inferences with this sort of design, which has recently been proposed to be meaningful, without any evidence. Let’s hope the required evidence is forthcoming so we can know if this confusion has been resolved.
Bad Models Are Out There
A paper recently came across my feed and I had the required data to replicate it in the U.S., but I ended up realizing pretty quickly that it was just overfit. The paper fit an ACCCCCCCCCCCCCCE model and concluded that C > A. The hope was to get at differentially shared C, but it arrived at its conclusions in the obvious and unimpressive way: by overclaiming about C through fitting it to every available degree of relatedness without a realistic means of identifying the constraints for different forms of C. This is not a serious design.
Another paper, by Kendler et al., entered my feed and it suggested that acknowledging differentially shared environments wouldn’t do much for the shared environmental contributions to drug abuse, alcohol use disorder, and criminal behavior:
Aggregate estimates of additive genetic effects for DA, AUD and CB obtained separately in males and females varied from 0.46 to 0.73 and agreed with those obtained from monozygotic and dizygotic twins from the same population. Of 54 heritability estimates from individual classes of informative sibling trios (3 syndromes × 9 classes of trios × 2 sexes), heritability estimates from the siblings were lower, tied and higher than those from obtained from twins in 26, one and 27 comparisons, respectively. By contrast, of 54 shared environmental estimates, 33 were lower than those found in twins, one tied and 20 were higher…. For the three externalizing syndromes examined, concerns that heritability estimates from twin studies are upwardly biased or were not generalizable to more typical kinds of siblings were not supported. Overestimation of heritability from twin studies is not a likely explanation for the missing heritability problem.
This is all fine and dandy, but I have been warned not to trust recent papers using half siblings in Swedish data. One notable issue for some of Ken Kendler’s recent papers featuring half-siblings is that each person can only have one legally-mandated registered address in Sweden. Thus, half-siblings who spend time together in different households can’t be captured in the data the way Kendler uses it. “Genes only” and “Genes + Rearing Environments” are increasingly wrong ways to think about younger Swedish cohorts, which include more half-siblings. The rate of shared custody with kids living with either parent on a weekly basis has increased from 1% in the early 1980s to around 30% closer to today. With this sort of data, it’s impossible to know how to specify the shared environment for paternal half-siblings in pedigree-based models.
Maybe Kendler et al.’s result is right, but I don’t know it. But I do know that data problems are real and underdiscussed, and bad models are both specified with good data, and results of bad data, even if, in theory, the models themselves are fine. Or in other words, some models are bad because they’re bad, and some models are bad because their underlying data is bad for them.
We Still Have a Lot to Learn
As noted above and in Footnote 9, for many phenotypes, we know that estimates of C line up across different types of twin and family models, but sometimes they might not. One notable example was cited by IB. In Frisell et al.’s comparison of the classical twin design, adoptee-parent, adoptee-sibling, and classical twin design-like sibling designs, they got somewhat different results across designs using and not using adoptees for the estimated heritabilities of violent criminal offending.
The point estimates for the twin and sibling models are indistinguishable and highly similar, and that’s a great and reassuring finding. But then the point estimates on the C variance (“Family environment”) were also lower for the adoptee models. The CIs were wide and they were incorrect when they went negative and the authors chose to truncate them at 0, but comparing the highest-powered model (“Sibling model”) to either adoptee model, the effect sizes were significantly different, as indicated using the incorrect 0 lower bound (p’s of 0.0035 and 0.0119 with the adoptee-sibling and adoptee-parent models). If we assume symmetry around the point estimates,14 this is no longer true for either model, as their estimates for the C variances are just too imprecise.
One explanation for this might be assortative mating, which would inflate C in the twin and sibling models, but not in the adoptee models. The coefficient for assortative mating was pretty large, at 0.40, but even casting off the random mating assumption, the effect on the point estimates was small and the difference between adoptee designs and the twin and sibling models remained, albeit becoming nonsignificant.
This brings me back to another issue mentioned at the beginning of the post: power is often really low. Knowing whether designs disagree about the extent of C is hard to ascertain, since the CIs from these structural equation models are so often wide. Even the Frisell et al.’s 1,521,066-pair sibling model had a CI on C ranging from 9% to 16%, and the twin model with 36,877 pairs had a nonsignificant estimate. Since small effects matter, knowing if these designs disagree by the small amounts pictured here is potentially important, but burdensome to assess. The only solution as I see it is to get larger sample sizes and to remain humble about what we know.
In yet another Kendler et al. paper, he and his colleagues found that estimates of C were heightened for twins compared to step-siblings and half-siblings. I have a thread illustrating this across different phenotypes here. This seems sensible enough: twin-specific effects include narrow cohort effects, residual age effects, etc. Twins should be more similar for environmental reasons than non-twins, even if only due to sharing the exact same age, since age corrections without large samples could easily leave behind residual age effects for individuals who are still undergoing development, as most samples of kids will be.
So, in this case, I imagine lower C for step- and half-siblings might be due to genuinely reduced sharing of the environment growing up, for various reasons. What this means for how C operates and what we should consider its level to be is still unclear. For example, what if twin-specific effects are different in terms of what cognitive skills are affected compared to the ones affected by sibling-specific effects? We don’t have good answers about any of this yet.
The role of age is also still not completely clear. We know that, with age, full-siblings and dizygotic twins are very similar. In the very large-scale data from Cesarini and Visscher which IB cited, the differences were minuscule and universally nonsignificant for adult measurements of traits. But minuscule is misleading: the intraclass correlations were consistently (excepting height, which could have been adversely affected by prenatal effects) somewhat higher for the dizygotic twins than for full siblings reared together.
We know dizygotic twin resemblance declines with age, explaining the Scarr-Rowe effect through the fadeout of C, and we even know that this explains some controversy about A potentially being lower than others had reported back in the late-1980s and 1990s, before the Wilson Effect15 was understood. For the foreseeable future, determining whether aging matters in other ways for understanding, say, interaction effects in samples with siblings instead of twins is probably not going to happen due to the inadequacy of available data.
Siblings who show greater age discrepancies may also have less comparable phenotypes for other reasons. For example, the if siblings are tested at the same ages, years apart, they might receive different IQ tests or the Flynn effect might have affected scores, boosting or reducing the score of the later sibling for artefactual reasons. Siblings are also more likely than twins to attend different schools entirely, so that might induce more variance in sibling comparisons. Twins don’t have these sorts of problems and there’s often not an easy way to adjust them away in sibling data.
People often presume that the Wilson effect and the fadeout of environmental effects are related things, but there’s no necessary relevance of the Wilson effect for specific environmental effect fadeouts in general, so it’s curious how this idea has propagated. It may be the case that these things are generally related, but no one has published anything with the data required to show they’re necessarily related quite yet. In an early draft of my Aporia article on genetic confounding, I even remarked that we really don’t understand the Wilson effect well at all from a causal perspective, so speculation about it and theorizing from it is often unwarranted. For example, do we know if and/or why the Wilson effect is accelerated with respect to IQ heritability for the less intelligent? Do we know if outcomes with more C in adulthood show reduced Wilson effects?
Group Differences in Variance Component Means
In a previous post, I showed evidence of Black-White differences in the means for the twin model A, C, and E factors for IQ scores in the U.S. This has important implications, as these differences allow us to directly ascertain why groups differed in their IQ scores.
Keep reading with a 7-day free trial
Subscribe to Cremieux Recueil to keep reading this post and get 7 days of free access to the full post archives.