The CDC reminds us that “Children from low-income households and those who live in housing built before 1978 are at the greatest risk of lead exposure.” Indeed, the NHANES has supported a positive association between poverty and blood lead levels (BLLs). And of course, both poverty and BLLs are negatively associated with IQ and positively associated with criminality — a fact taken for granted nowadays.
The potency of these factoids has made lead a go-to scapegoat for the problems of the poor, Black, etc.
Inconveniently, recorded BLLs in the United States haven’t been meaningfully differentiated by race or class since the earlier 20-teens.1 This reality coupled with the fact that BLLs haven’t been elevated to a very harmful degree in any major group for more than twenty years makes it a wonder that the national conversation on equity seems to be more polluted by lead than the real world is.
Lead is a media darling that refuses to stop hogging the spotlight. Take Flint, Michigan. In 2019, even someone so invested in the issue of lead abatement as chief leadocrat Kevin Drum acknowledged that the city’s problems had largely passed.
This is very sad: Marc Edwards, the Virginia Tech professor who first exposed toxic levels of lead in the water supply of Flint, Michigan, was initially a hero to the Flint community. Thanks to him, Flint became the target of nationwide outrage, and steps were finally taken to reconnect Flint to the (safe) Detroit water supply. In less than a year, lead levels in Flint water had dropped to safe levels.
So what did Edwards do? Well, he’s a scientist, and just as he had honestly exposed Flint’s problems in the first place, he also continued to honestly report the results of the intervention. When the water was once again safe, he said so—and that turned him from a hero into a pariah.
Skip ahead
So here we are: anti-science, tribal, and subservient to our most extreme wing. Oh, and a guy named Marc Edwards, who exposed this disaster and got it fixed, is now practically an exile. It’s a sad microcosm of our modern political arena.
As of late-2022, the Michigan Department of Environment, Great Lakes, and Energy reported that Flint had reached the milestone of replacing 95% of its legacy lead pipes. In other words, Flint is now comparable to much of the rest of the country and it’s even ahead of some places, but let’s stay focused. What does the data on BLLs look like? Here’s race:
And here are BLLs by a proxy of class:
So if lead really isn’t a race or class problem anymore, what’s the deal? In a single word, it’s confounding: Wherever people have high levels of lead exposure, they are poor, they come from underperforming minority groups, and they have high burdens of mental illness, but these things are (mostly) not due to lead.
The confounding of lead effects is genuinely dumbfounding. The extent to which associations with lead are confounded with parental characteristics, socioeconomic status, race, etc. is so profound that today, after more than fifty years of extremely vigorous study, we have no idea what the effect of lead is on IQ, let alone criminality, mental health, socioeconomic attainment, or basically anything else.2
Fortunately, because the world took a stand against lead, we know confounding is undeniable.
Methods and Background
Here’s how this works. First, we acknowledge that lead levels have varied over time, and they've trended down since the late-1970s. A major source in the past was tetraethyl lead in gasoline, but there were also contributions from paint, lead weights, etc. Once those things were banned from production and removed from homes, BLLs began their rapid descent.3 Take a look:
Second, we focus on something lead has been proposed to affect. Since it’s well-known and well-documented, let’s use IQ.
Gregory & Mohan (1977) and their references will supply the studies for what I’ll designate the “Early Era of Lead Research”. This is the first major time in which the effect of lead on IQ was studied. The “Middle Era of Lead Research” will be indexed by Kaufman (2001), and studies from 2002 onwards will index the “Modern Era of Lead Research”.
Third and finally, I will use the studies from these eras to establish how much 1 μg/dL of blood lead has been proposed to affect IQ at different times.
The following paragraphs contain various methodological and data details. Those who are not interested in them can go down to the bold heading of the next section.
When lead levels for control groups were not included for a study, such as in some of the studies Gregory & Mohan discussed, I imputed the mean for a given sample age, sex, race, and poverty composition from the nearest NHANES year. When an IQ metric was atypical (i.e., “mean 50, SD 7.5”), I converted it to the standard IQ metric (mean 100, SD 15). With atypical tests, I attempted to find a score conversion to a more typical one and to aggregate results accordingly.
Studies without control groups or lead effect coefficients (i.e., r's with corresponding summary statistics or β's) were not included for the obvious reason that they did not provide a means to compute the effects of lead exposure.4 I could look for other studies from the same times that use the same tests or for those tests' norming sample summary statistics, but such data doesn’t usually exist or isn't well enough described to genuinely reuse if it lacks control data anyway, so there’s little point wasting time looking for one or two instances where I can fill in data.
Studies like Dike et al. (2020) were omitted because they did not provide BLLs, but instead provided ingested lead levels.
When dentine lead levels and BLLs were available, BLLs were used; when only dentine lead levels were available, they were used, as they should still be valid indicators of at least lifetime lead exposure. They are highly correlated with BLLs and analyses with both available show little average discrepance.
When multiple ages of data were provided, the latest with an IQ test was used even though this always led to more limited sample sizes because of sample attrition. I did this because I wanted the most up-to-date data with the lowest measurement error for the IQ measure in each case. Regardless, even when using the earliest available data in studies where I had this option, the results were practically unaltered.
Studies that only provided regression or correlation coefficients were not used for calculating case/control gaps, and for that reason, case/control gaps had wider standard errors than the estimates of the effect of 1 μg/dL of BLL.
The effect in an era and the case/control gap in an era were the results of inverse variance-weighted meta-analyses of that era’s studies.
The summary details for each lead research era’s samples were as follows:
Early Era: 1963-1975, N = 822, K = 11, mean BLL = 47.34
Middle Era: 1982-1999, N = 6,789, K = 30, mean BLL = 13.18
Modern Era: 2002-2020, N = 12,288, K = 46, mean BLL = 2.33
What is the effect of 1 μg of lead on IQ?
Good studies from the different research eras can be used to illustrate how lead effect sizes have changed over time.
Landrigan et al. (1975) represents the Early Era. In this study, there were 46 children in the high lead group and 78 in the control group. Their respective BLLs were 48.3 and 26.9 in 1972 and 40.5 and 26.5 in 1973, and they were 8.3 and 9.3 years old, respectively. So we have a gigantic 14 μg/dL gap between these groups. The high lead group had an average IQ of 88.02 versus 92.88 for the low lead group, or a 4.86 point IQ gap, and thus a per μg effect of 0.35 IQ points.
Baghurst et al. (1992) represents the Middle Era. In this study, there were 494 children who had IQ results, and they were divided into quartiles by BLLs. The mean concentrations of blood at assessment age were 6.6 μg/dL for the lowest quartile, 10.1 for the second, 13.7 for the third, and 20.0 for the final one. Their IQs were 109.6, 107.7, 102.7, and 98.7, respectively. Going from the lowest to the highest lead exposure quartiles, we have a BLL difference of 13.4 μg/dL and an IQ difference of 10.9 points. Going quartile to quartile, the effect of 1 μg of lead was 0.54 IQ points, 1.39 IQ points, and then 0.63 IQ points, with the aggregate (1 - 4) being 0.81 IQ points.
Kim, Yu & Lee (2010) represents the the Modern Era. In this study, there were 302 children who were median-split by BLLs. The high BLL group had a mean BLL of 3.74 and the low BLL group had a mean of 1.92 with IQs of 106.4 and 110, respectively. These differences of 1.82 μg/dL and 3.60 IQ points mean that the per μg/dL IQ drop was 1.98 points.
The first study was from an era where there were much higher average BLLs and sources of lead contamination were more common in general. That’s why, besides small sample sizes, this era is the only one in which there are numerous studies with estimates of beneficial effects of lead and largely nonsignificant results. The effect of everyone being more capable of becoming heavily exposed to lead regardless of socioeconomic status was that the effect sizes were all over the place. You can see this in many of this era’s studies reporting socioeconomic information: they consistently showed the socioeconomic stratification of BLLs was reduced in this era of ubiquitous lead exposure. Landrigan’s study had an above-median effect for the time.5
Midway through abatement to modern levels, the effect of lead had already grown, and Baghurst et al. had a below-median effect for its time.
Clearly, the Modern Era of lead abatement had been met by both low BLLs and claims of extreme lead effects. With that said, I picked this study to push the point home, since Kim, Yu & Lee had a below-median effect.
What about the overall results?
In studies covering samples from 1963 to 1975, an increase of 1 μg/dL in BLL was met with an IQ decrease of 0.035 points. This era had by far the highest proportion of null and negative results, but it also had smaller sample sizes. In this era, there was no correlation between effect sizes and standard errors (r = -0.06); publication bias was absent.
In studies covering samples from 1982 to 1999, an increase of 1 μg/dL in BLL was met with an IQ decrease of 0.358 points. This era had larger sample sizes, but it also had considerable publication bias, with a correlation of r = 0.42 between effects and their standard errors. This is a marginally significant correlation, but it suggests large publication bias corrections are needed.
In studies covering samples from 2003 to 2020, an increase of 1 μg/dL in the BLL was met with an IQ decrease of 3.631 points. This era had the largest sample sizes, by far the most nationally and racially diverse samples, and the worst publication bias, with a correlation of r = 0.71 between effect sizes and their standard errors.
The effect of 1 μg/dL of blood lead in the most recent era of study is 103.74 times larger than it was 40 years prior.
Why did this happen? Three bad explanations
The effect sizes in the literature on the relationship between BLLs and IQs didn’t skyrocket for no reason. Before elaborating on the reasons I believe are true, there are several explanations that come to mind that are worth a mention.
Sensitivity to lead has increased over time.
Lead genuinely does not matter much between 10 μg/dL and lead poisoning.
Lead effects are strongly nonlinear.
First: There is simply no reason to believe people have become more sensitive to lead over time and there is no way to make this idea even remotely plausible without something like an increase in another lead augmenting chemical’s prominence. There are no such candidate chemicals to my knowledge.
Another interpretation of this alternative explanation is that lead has changed qualitatively over time or the interpretation of BLLs has drifted. These options are likewise unsupported and they come with no reason to think there’s anything to them. Consequently, I am dismissing this explanation out of hand.
Second: Plenty of studies do appear to show effects beyond 10 μg/dL. In fact, the whole middle era was about effects that were mostly just beyond the 10 μg/dL level. When modern studies exclaiming that there are nonlinearities are examined, they seem to offer support for limited effects beyond 10 μg/dL only because what they really show is mostly normally distributed, variously-confounded BLLs with increasing range restriction as mean BLLs decrease because people cannot have BLLs below zero.
This produces nonlinearities — most often in the form of a shift to a flat relationship between IQs and BLLs past a certain point — because as the mean BLL shifts towards zero, the right tail of high BLLs is populated proportionally less by people who are exposed to lead for the same reasons as people within the new normal range (i.e., the known-confounded reasons), and more by people who are exposed for reasons that are accidental, random, or in a word, noisy.6 Most of these studies also do not find evidence for significant nonlinearities, and the ones that do primarily do so by fitting every nonlinear term under the sun until something seems to fit.
The chance nature of today’s extremely high BLLs — yesteryear’s normal — is why the modern big effects seem to be around the mean (i.e., <10 μg/dL). What we have is constant mean differences for confounding factors like socioeconomic status and race alongside decreasing absolute, but not so much relative, differences in BLLs across studies. As the differences in BLLs decline and the differences in IQ remain unchanged, the amount each BLL must explain necessarily has to increase.
There are three more things to say about this. Firstly, studies like Canfield et al. (2003) and Jusko et al. (2008) actually plot this. There’s a high-density part of the plot, and then there’s the low-density, allegedly nonlinearity-supporting part you get from trying to assume that the reasons for lead exposure are interpretable all the same at today’s extreme tails. Take a look:
These studies also provide quantification of the effects within various ranges. For Jusko et al., the effect of lead on IQ is 1.2 points per μg/dL below 10, 0.32 between 10 and 20, and 0.15 between 20 and 30. For Canfield et al., the lifetime average effect of each μg/dL of lead is a loss of 0.87 points in the whole sample, and 2.42 restricting to below 10 μg/dL: in both cases, their quantitative conclusions were supported by small N’s in the tails.
Second, the early literature has several studies in which the authors suggested very substantial importance for differences in lead levels among the highly exposed. As Schroeder et al. (1985) claimed in their supposed replication of Bellinger & Needleman’s (1983) result (itself an attempted replication of Perino & Ernhart’s 1974 work, but cf. Ernhart, Landa & Schell, 1981),
Another indirect test of an effect of lead on child IQ might be to examine its effect on the relationship between maternal and child IQ. According to the [polygenic] model of [the heritability of] intelligence, one would expect the correlation between maternal IQ and child IQ to be about 0.50. Lead might disrupt this relationship, as has been found by Bellinger & Needleman [Note: their result was not significant]. A similar result was found in the present studies. In the initial study, the correlation between maternal and child IQ for the children with blood lead levels of 6-30 μg/dL was 0.528; for children with blood levels of 31-56 μg/dL, it was 0.058. At five-year follow-up, when all blood lead levels were at or below 30 μg/dL, the correlation was back up to 0.45…. [It] can be seen that about half of these children had blood lead levels above 30 μg/dL and half below that level in 1977-1978.
Clearly these extreme BLLs were proposed to be doing something quite strong, because to change a correlation requires a large effect.7 Based on this sort of commentary, substantial importance had been given to differences at extreme BLLs, and this was unfortunately not the oddest example.
Third, using data from earlier eras where plots are included or datasets are available, larger effects are not observed in the 0-10 μg/dL range. In fact, the relationship in the early and middle eras in that range and the even-more-extreme-than-today right tail is usually flat in the same way that the relationship within the right tail of BLLs today appears flat. The noisy area in any era is usually going to more often produce null relationships. The resulting artefactual nonlinearity thus can and should be ignored.
Third: No individual studies have vindicated strong nonlinearities and there is no biological mechanism to support them. Nonlinearities mean dose-dependent effects/lead sensitivity and, while interesting to think about, the only piece of evidence in their favor is the meta-analytic result I’ve shown here where the whole of the evidence is derived from looking across eras, and as shown, it cannot be interpreted as supporting strong nonlinearities. Evidence for the confounding angle as the explanation is strong, however, and it’s why, rather than mechanistically improbable protective effects, you get results like this:8
Why did this happen? A good explanation
The real reason the relationship between lead and IQ has exploded is two-fold:
Consistent patterns of confounding. The factors disposing one towards higher BLLs and lower IQs have been constant across the whole of the research literature. Moreover, the effects those lead exposure-disposing factors have on IQ have been mostly constant, and at the very least, directionally consistent in their effects. Higher class still disposes to higher IQs today, being Black still disposes to lower IQs today, having smarter parents still disposes to higher IQs and vice-versa, etc. etc. With BLLs down and the factors driving the relationship in the earlier literature still around today, one can sample those groups, see the BLL gap has fallen, and produce a spuriously extreme estimate of the effect of lead because the gaps driving the relationship are still around just as much as they’ve ever been while the lead is mostly gone.
Publication bias. There is a strong, negative sentiment towards lead and in favor of lead abatement and there may also be a strong editorial incentive to reject publications that produce null or positive relationships with lead. As the issue of lead abatement has become more politically salient — and it certainly has at least post-Flint — publication bias has worsened. Given that publication bias worsened over time in the present meta-analytic results, this supposition is clearly vindicated.
Because the people want lead as a bogeyman for public action, of course the effect of lead had to remain significant. The effect of lead became more extreme and exaggerated since that was the only way results could stay significant. The other way for new results to remain significant would be to increase sample sizes to detect smaller effects, but sample sizes increased more between the early and the middle era than between the middle and modern eras. To get to the effect sizes observed in the first era with the extreme extent of modern range restriction in BLLs would necessitate thousands of people per sample and reduced confounding.
BLL differentiation by race, class, etc. has, as shown earlier, begun to disappear in aggregate. But publication bias allows this to be defeated to deliver strong lead effects today. All a would-be lead-effect-finder has to do is sample from an area where, for example, impoverishment is still related to lead exposure to whatever degree is necessary, or where certain races still predominate in neighborhoods with older homes. This can work even if the trend for the whole population is towards equality of BLLs. And if a researcher fails in their endeavor, all they have to do is avoid publishing it. Only successes have to enter the literature, and perhaps only successes get to enter the literature.
Theory Anchors
I believe the case I’ve made is strong. The statistical mechanism that explains why effect sizes have blown up heavily implicates confounding with lead levels as the primary explanation for the perceived effect of lead, and patterns of publication bias are, indeed exactly as expected if this theory were correct.
However, some people may still be unconvinced.
A final supposition should help to anchor my explanation to the facts while standing in the way of alternative explanations. This supposition is as follows:
We know both race and class were related to lead, and we know how and to what degrees. Since lead abatement efforts have eliminated socioeconomic and racial differences in blood lead levels, the intelligence gaps between these groups must have also narrowed.9
Let’s first discuss racial differences. Black BLLs were massively elevated over White levels until very recently. Before 1946, roughly 22% of Blacks had BLLs >10 μg/dL compared to roughly 6% for Whites. In the period 1946-1973, 14% of Blacks had BLLs >10 μg/dL versus 1.4% of Whites. And between 1973 and 1994, 3.4% of Blacks and 1.5% of Whites had BLLs >10 μg/dL.
If we use the midpoint of the middle and modern era estimates of lead effect (1.99), we can calculate the expected effect on the Black-White gap.10
Here is the CDC's presentation of NHANES data. If we use the ages 1-5 data in Table 2 (Table 3 for ages 6-11), we see that between 1976 and 1980, Blacks had a mean BLL of 20.3 versus 13.9 for Whites (16.2 vs 12.0). In the 2011 to 2016 column, Blacks had a mean BLL of 1.1 versus a White BLL of 0.8 (0.8 vs 0.6). If the effect of 1 μg/dL of lead is the loss of 1.99 IQ points, then Blacks should have closed the IQ gap by 12.14 IQ points (7.96).11
As La Griffe du Lion said some 21 years ago, the fundamental law of sociology is that
On large-scale tests of reasoning ability, the observed mean difference between non-Hispanic whites and African Americans is 1.1 +/- 0.2 standard deviation.
For which he noted the following results:
These studies had a simple average average of 1.13 d12. A then-recent publication confirmed a gap of this size in a gigantic meta-analysis and provided us with a confidence interval for an estimate of 1.10 across all tests of 1.06 to 1.15. These gaps have been largely invariant over time to the type of test and the Flynn effect has not had racially heterogenous effects in the U.S. As an example of a test that has been administered over a very long time period, the Wordsum produces this result:
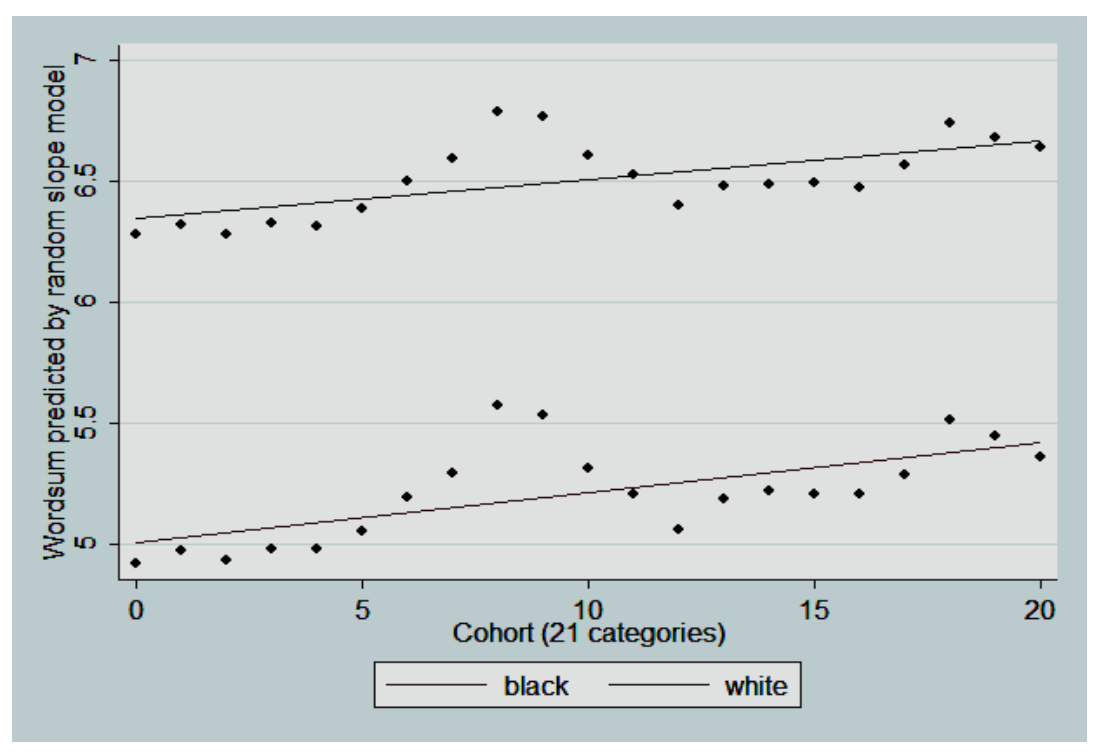
Recent studies that have involved samples from after BLL differences between Blacks and Whites closed have produced similar results:
Kirkegaard et al. (2019) used a cohort with data gathered after 2010 and found a gap in general intelligence between Blacks and Whites on the order of 1.09 g/1.10 d.
Lasker et al. (2019) used a cohort that was gathered between 2010 and 2013 and found a gap in general intelligence between Blacks and Whites on the order of 1.05 g/d.
Fuerst & Connor (2021) also used a post-2010 cohort and found a gap in general intelligence between Blacks and Whites on the order of 1.06 g/0.97 d.13
The simple averages for the post-lead abatement datapoints are 1.06 and 1.04 g or d, respectively.
A gap of 1 d is equivalent to a 15-point gap. Since this has been the gap for as long as it’s been recorded and it remains that size in the most recent, post-lead equality data and the observed lead abatement was supposed to take out almost half to three-quarters of it with the lead literature’s estimates, something is wrong.
Or something would be wrong, if you assumed the effect size for lead in the literature was a fully causal and accurately measured effect of lead on IQ. If you believe there’s artefactual influence involved in the estimate and, more strongly, that the relationship may not be causal, then there is no issue.14
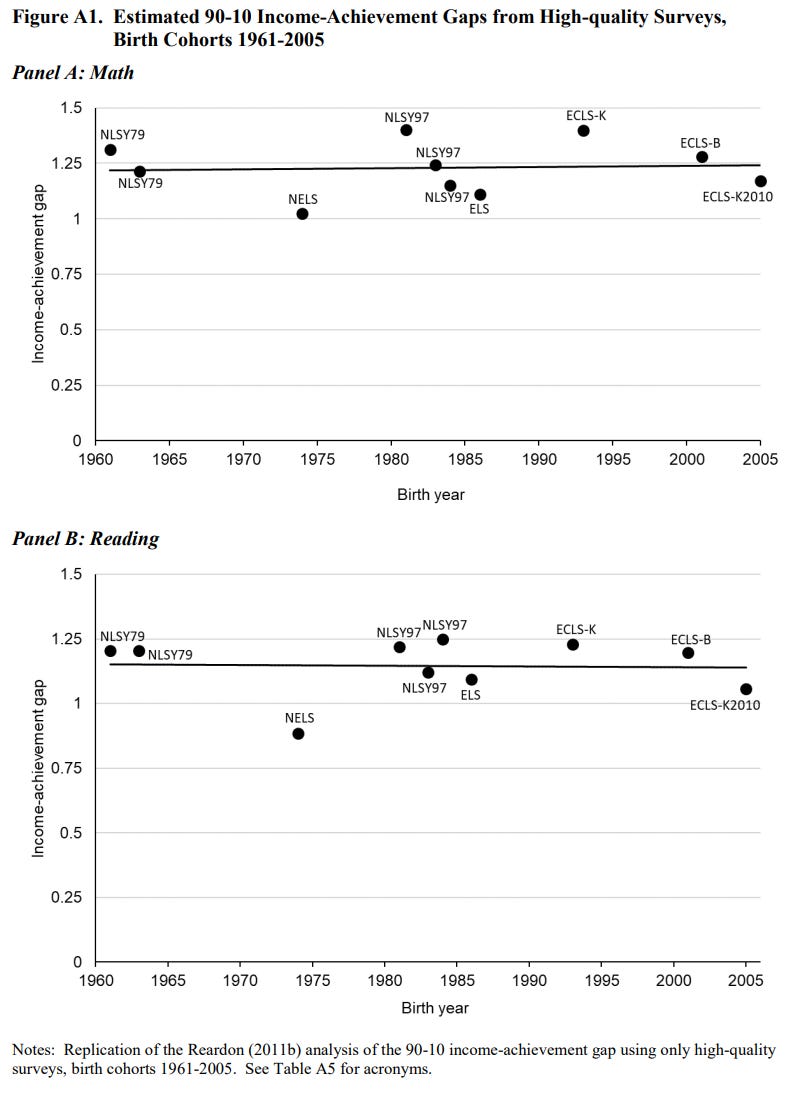
Now let’s talk class differences. They’re large and like racial differences, they’ve been large for as long as they’ve been recorded. Take the following plot from Hanushek et al.’s preprint on long-run trends in achievement gaps by socioeconomic status.15
In some of America’s best surveys, the gap between the 90th and 10th percentiles of income didn’t budge at all between 1960 and 2005. Hanushek et al. also included data from several other achievement assessments with their preferred 75th percentile vs 25th percentile gaps provided.
If anything gaps by socioeconomic status seem to have trended up over time, but this is only something that seems. In reality, the various tests’ psychometric characteristics or their samples differed in ways that created an illusory trend. Controlling for the specific test, the trend becomes a nonsignificant 0.001 (p = 0.418) rather than the apparently significant r = 0.363 (p = 0.008) in that picture. That said, the conclusion is the same: like the Black-White differences in IQ, we should have seen very substantial gap narrowing.
Because the differences by socioeconomic status in IQs were larger, but the differences in BLLs were even larger yet, we should have seen a staggering level of gap reduction. Just using the income-to-poverty ratio used by the CDC, we should see a bit less impressive but still detectable gap reduction of 6.57 (2.99) IQ points. Yet we either do not, or we have too little power to detect a change.
In fact, though it doesn’t have any implied value for anchoring this explanation, the difference between cases and controls in different eras was also pretty consistent.16
Without strong nonlinearity, the gaps should have declined over time as the absolute gaps in BLLs between cases and controls did. This points yet again to misestimated, largely or completely noncausal lead effects and a misleading literature built around them.
Where does this leave us?
With all said and done, it is abundantly clear that the effect of lead on IQ is overestimated and studies claiming that there’s no lower-bound for negative effects have not been adequately testing their hypothesis. Instead of effects of lead, what they've really been testing has largely been stratification of lead exposures by various causes of variation in IQ. Without something like twin or sibling controls or high-quality longitudinal data, it is dubious whether lead effects can be properly estimated at all.17
More importantly, such studies will continue to produce the wrong conclusions as the mean BLL moves down and some degree of social stratification of lead exposures remains, or at the very least, can be found and exploited by researchers. To this end, they can, and I believe will, be used to justify permanent intervention in the name of lead abatement. The effort will never end, even when BLLs are so low as to be clearly meaningless for any outcome people might be interested in. Or in other words, the literature claiming lead effects on various outcomes stands as a prime example of social science as a justification for indefinite social action.
To keep up with the public’s demand for lead’s harms, the effect of lead has had to needlessly explode. Since the public does not internalize that problems it learns about are ever truly fixed, this will continue so long as the public continues to imagine lead is a problem and people are motivated enough to repeat the same analyses, with less and less realistic results, forever.
In a sense, the lead-social outcome literature is the perfect example of the de Tocqueville effect. People anchor to a problem and refuse to let go, resolved or not. Because an issue is important to them, as the problem diminishes into life’s background, they cope by making the issue look far larger than it ever was. The fact that the effect sizes for lead increased as the problem diminished is an amusing statistical rather than personal example of the effect cropping up.
This CDC presentation is also worth a cursory look.
Indeed, in a study supporting the “well-established age-crime curve”, when socioeconomic confounding is removed from the picture, the effect of lead on criminal perpetration adds little to the effect of being male, and the effect is not particularly large anyway. That first dataset also provided marginal evidence for an effect of lead on socioeconomic mobility, but it is unfortunately uninterpretable as it stands because of the use of too many measures of the same thing (i.e., g) in the focal regression.
None of these should ever have been used to inform the lead literature. Some are truly egregious. For example, take Pueschel, Kopito & Schwachman (1972). In a mostly Black sample, the average IQ was 86, which, with a sample of just 58, is indistinguishable from the 85 IQ average for Blacks in general. This variety of study that exploits the fact that Blacks had high rates of lead exposure due to their high rates of pica (where “eating paint chips” comes from) and they had low IQs was unfortunately not alone in the literature.
Early results were very slightly but not significantly overestimated because I included Perino & Ernhart (1974). As Ernhart, Landa & Schell (1981) and Ernhart, Landa & Wolf (1985) showed, the data in Perino & Ernhart needed to be better controlled, and the effect they found disappears with reasonable adjustments. Since the original study still receives more citations than either correction, I aimed to discuss confounding, and the study’s sample was still an early era one, it seemed reasonable to keep it in the era and interpretation it was in.
By analogy to IQs, the two types of mentally retardation are “mild” — caused by the normally-distributed causes of the IQ distribution in the general population, including additive genetic effects and random environmental stimuli — and “severe” — caused by things like bricks to the head or rare aneuploidies. The behavioral characterization of these types of retardation dramatically differs, with “mild” cases showing clearly superior adaptive behavior compared to “severe” cases.
The contrast between these two types of retardation also provides insights into their causes. Both old and new data shows that the siblings of people with “mild” retardation are midway between their retarded sibling and the general population. It makes sense: they share the genes that caused the retardation. The same thing is observed for basically all polygenic conditions, from autism to asthma (as continuously measured via lung function tests). But, for “severe” retardation, the distribution of sibling’s IQs perfectly matches the general population. And it should! Why would a person whose sibling became retarded due to a baseball bat lead their sibling to be any different?
This discontinuity in causes leads to a bump at the low end that is not accompanied by a similar discontinuity and bump at the high end for IQs. The reason is simple: throwing a wrench in a machine will tend to ruin it, and only far more rarely improve it.
Assuming you want to bring a correlation of 0.528 down to 0.058, you need an effect size of 1.25 d. In their sample, there was no relationship between lead and IQ on either side of a BLL of 30 μg/dL; something was only there with the whole group, and that something wasn’t a strong relationship, so this effect had to be basically miraculous to cause such a split while not producing any other evidence that it mattered.
Someone with access should perform a sibling-controlled analysis of lead effects with their data.
One could exclaim in an ad hoc fashion that some countervailing force maintained the exact effect that lead abatement fixed, but such an argument is pure pseudoscience. This supposition also applies to other gaps, like those in criminality and mental health.
Another anchor I did not discuss in this study was the relationship between parent and child IQs. High lead levels have been proposed to reduce them, but they have not budged despite abatement successes.
The effect of lead does not appear to differ by race, but when disaggregating by race, the effect is reduced by nearly a quarter for both groups. Since my goal was to showcase the extent of confounding, I did not disaggregate the meta-analytic data in this way.
If there’s a nonlinearity above 10 μg/dL — and there’s no god-given reason there should be —, then the expected gain for Blacks could be reduced.
I have provided a plot of the comprehensive data up to a fairly recent point, here. It is also worth noting the the lead-IQ literature fails to make sense of Asians or Hispanics, who have higher IQs and higher BLLs and lower BLLs and lower IQs when respectively compared with Whites.
Even a British sample gathered via Prolific in 2022 found a gap of 0.99 d.
The only way to escape this awkward conclusion regarding the true effect of lead is to propose that something else acted to increase the racial gap just as much as lead should have reduced it. That, race-specific effects, or nonlinearities that are so strong they render gap closure nonexistent or at least undetectable, are all viable candidates, if virtually untenable in light of the existing evidence.
Interestingly, datasets like Miranda et al.’s (2007) show the classic pattern of explanations that fail to explain group differences because they’re explained by regression to the mean. Take their Figure 3: the Black-White gap is somewhat reduced when stratified by BLL, but there is still a constant gap between the races and the difference in mean BLLs is enough to recover the whole gap. If, like education, this does not represent causality, then convergence in mean BLLs should fail to disrupt this pattern and the differences will remain.
As a final addendum, if this study’s conclusion that the effect of lead exposure is not an effect on general intelligence, g, is correct, then lead abatement cannot fix the Black-White gap, as the Black-White gap is due to g, whereas the lead effect appears to be unrelated to g.
In a more recent version of this preprint, they have removed this figure and their 75-25 gap plot has been “controlled” in various unclear ways and four datapoints have been removed with the result being that they managed to turn the trend negative. I elected to plot the uncontrolled SES-achievement gap because that is what is actually available and salient. I also have limited trust in controls and think many of them are frequently spurious. Hanushek et al.’s decision to control for fixed effects at the school level feels like it may be just that.
This plot looks like it does because increasing proportions of studies presented β’s and r’s instead of case and control data, and case/control differences became less meaningful and much closer in terms of BLLs. In the past, they were natural groups like people living near smelters versus those living away from them, or people living near curbs versus not. Nowadays, groups are often just results of median splits or other atheoretical groupings.
Several studies included follow-up IQ and BLL data and the meta-analytic relationship (k = 7) between changes in BLLs and IQs at follow-ups for usable studies was not significant (r = -.10). This is about as close to a longitudinal analysis as seems presently possible.










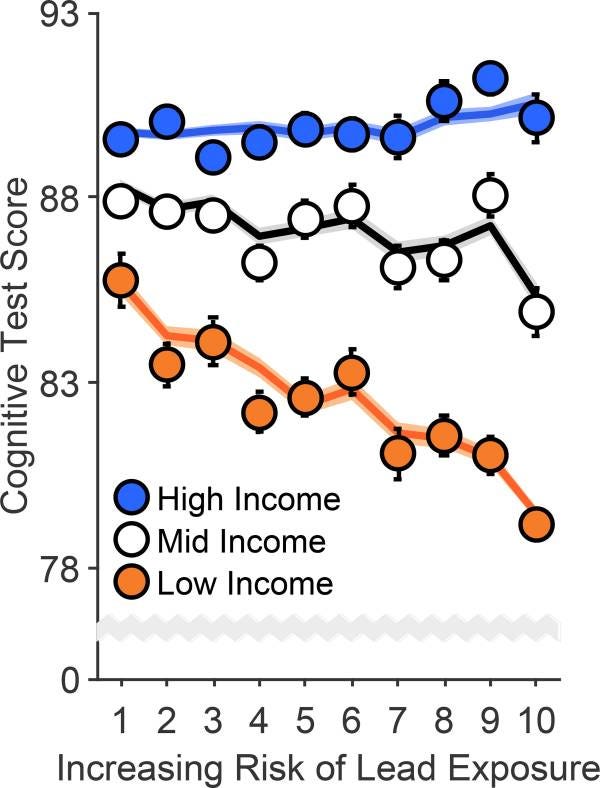



Indefinite social action indeed. The CDC states “No safe blood lead level in children has been identified.” Based on that logic, even if blood lead levels drop to ng/L or even pg/L, they’ll still be “too high.” Thank you for the very interesting post.
My impression is that in Southern California there is a negative correlation between the prestige of a school, public or private, and it's proximity to a freeway. In the San Fernando Valley, the well-known schools tend to be located near the 101 Freeway and the less prestigious schools are off in the hinterlands.