Education Isn’t What It Used To Be

How smart do you have to be to get a degree? How much school do you need?

It sure looks like the education system is melting down, doesn’t it? Just look at this:

Jensen (2023)

Are schools failing us? Are we getting dumber?

What if I told you that the population mean was 100 throughout the entirety of the series in this image? Well, it really is.

The only thing that changed was that education increased. As education increased, some of the more intelligent people who would have attained lower levels of educational attainment moved up to the higher ones, bringing both groups down in the process. This is the “Will Rogers Phenomenon,” best encapsulated by the whimsical line “When the Okies left Oklahoma and moved to California, they raised the intelligence level in both states!”

The Will Rogers phenomenon is a real thing that shows up all the time. For example, during the Great Migration, African American migrants who left the South had more European admixture than those who stayed behind, but less European admixture than those already living in the North. You might have seen this recently:

Dworak, Revelle and Condon (2023)

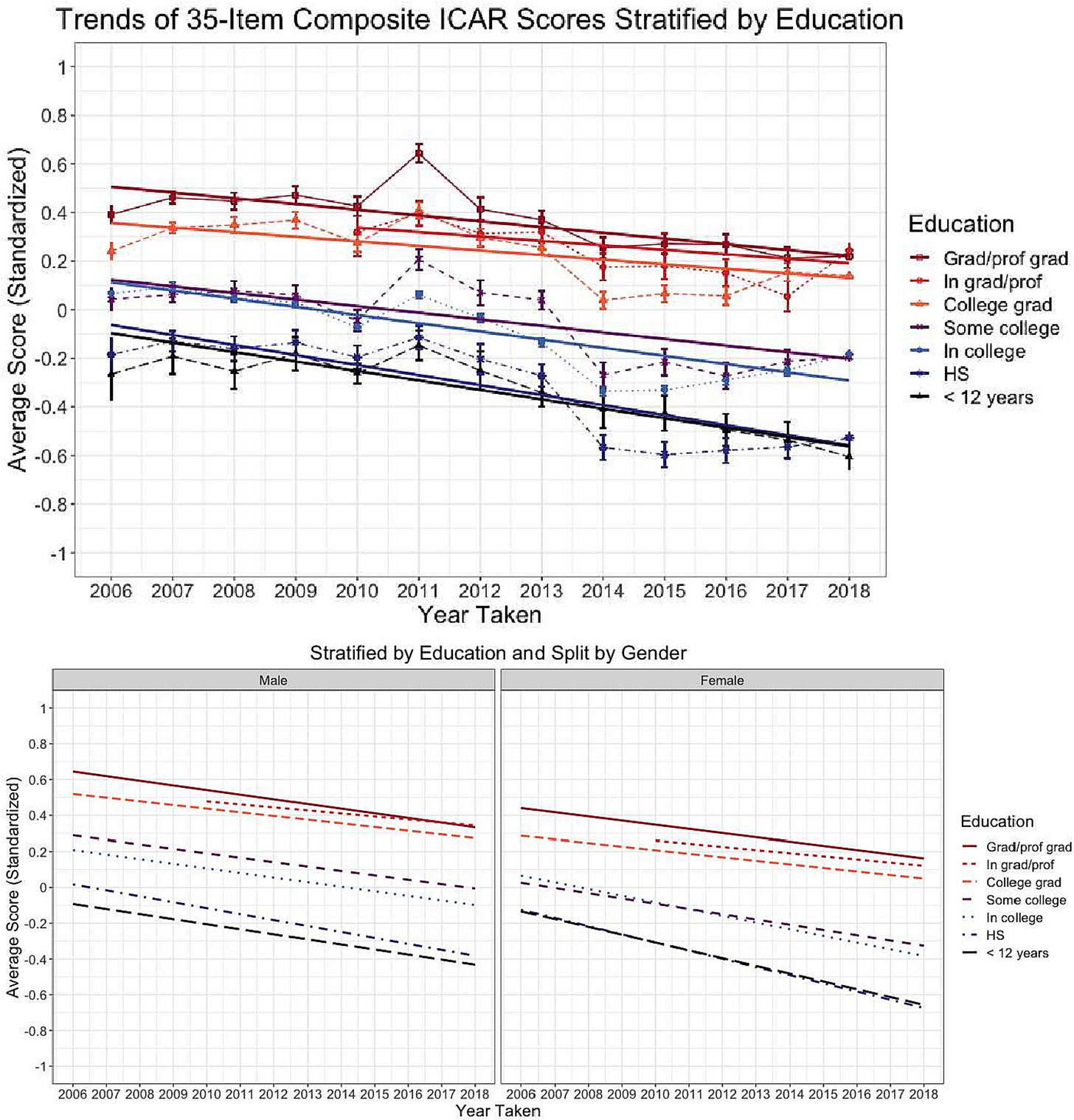
We can see the Will Rogers phenomenon at work in this instance because the overall slope was -0.015 standard deviations per year. For those with less than twelve years of education the slope was -0.039, whereas for high school graduates, the slope was -0.041. For those attending college the slope was -0.034 versus -0.027 for people who had some college but didn’t graduate; the slope was -0.019 for college graduates, -0.018 for those currently in graduate or professional school, and -0.024 for those with graduate or professional degrees.

The overall slope is less than the slope for any individual level of education because people are sorting across the levels in exactly the way I suggested.

So, are we getting dumber? Unfortunately, this wouldn’t show it. If the authors ever release or return to the data to analyze whether the changes are measurement invariant and how they appear after post-stratification, then we can know. Until then, we’ll be left guessing.

---

Controversy at the Frontiers of Psychology

Many of you have probably seen or heard about a paper entitled “On average, undergraduate students’ intelligence is merely average.” Shortly after the paper’s abstract went live online, it accumulated an Altmetric score of over 1,600, over 50,000 total views at its journal, and more than 2,000 posts on Twitter.

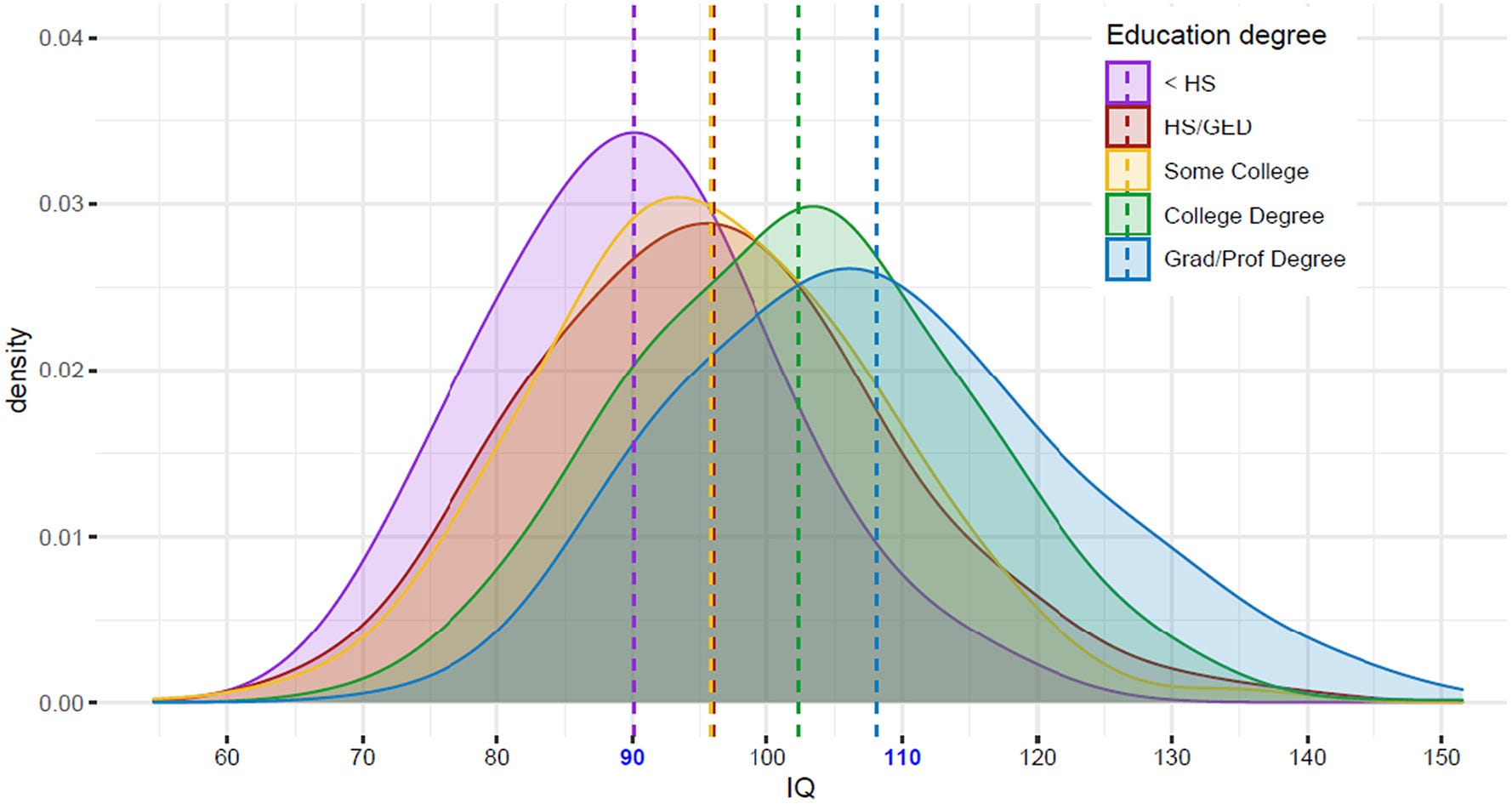
The paper described how, over the past century, tertiary education has gone from a cognitively elite affair to a decidedly average one. In the distant past, those who attended university had very high IQs; nowadays, they’re only slightly above-average. Take a look:

Befitting a paper with such a high level of popularity, Frontiers in Psychology retracted it immediately after it was accepted.

The reason for the paper’s retraction that was provided to the authors was that “a number of overstated claims were brought to the attention of our Research Integrity team.” What the claims were isn’t clear from this description, so the paper’s authors asked what the problems were and why a paper that had been reviewed and accepted was suddenly no longer acceptable. They also asked why they hadn’t been refunded the article processing charge of $3,295. A few days later, they received the reply that “The reason for the decision is: The manuscript could not be sufficiently revised by the authors to address the concerns by the reviewers or editors during the review process.”

This is not a very clear explanation.

One explanation I might consider acceptable is that the samples in that chart aren’t representative of the broader undergraduate populations. But this isn’t a good enough explanation for two reasons. Firstly, we have a strong prior on this finding.

Consider the known and substantial increase in educational attainment over time. This increase in educational attainment has been accompanied by an increase in its heritability:

Increased heritability means increased equality, as it implies the environments we come from matter less than they once did.

The thing connecting educational heritability to equal opportunity is declining selectivity:¹ if there’s an ability threshold for entering university, the importance of sibling differences for educational attainment are magnified near it. As the threshold falls, siblings whose antecedent traits are correlated can allow them to become more correlated in terms of the thing that varies over that threshold which is, in this case, educational attainment. But this also means that, now, the lower-ability siblings goes to school when they wouldn’t have before.

This may sound like it should increase the variance due to the nonshared environment, but as we can see in the video above, the variance that really plummeted lately was from the shared environment. This all fits together because parents can help kids to achieve a higher level of educational attainment than their endowments would typically allow. Moreover, they tend to invest disproportionately in lower-performing siblings. Consider the following:

• Nicoletti and Tonei (2020) found that parents reinforce the high socioemotional skills of their children by spending more time socializing with them, and they compensate for a child’s low cognitive skills by increasing the time those children spend in learning activities.

• Terskaya (2023) found that parents seem to be averse to inequality within the family. As a result, they seem to work to attenuate the downsides of a child’s disability on their educational attainment by investing more in disabled than nondisabled children.

• Sanz-de-Galdeano and Terskaya (2023) found parents of non-twin siblings seem to be averse to inequality: even without knowing about their kids’ genetic endowments directly, they seem to invest more in the child with the lower polygenic score for educational attainment. However, they do not seem to display this tendency for dizygotic twin siblings.

• Consistent with these findings, Johnson, Deary and Iacono (2009) found greater shared environmental variance in educational attainment at low IQs. Similarly, Beauchamp et al. (2023) found evidence for an effect of family socioeconomic status on the educational attainment of Korean adoptees and evidence for a negative genetic interaction between family socioeconomic status and educational attainment polygenic scores for measured IQ scores. That means that family socioeconomic status partially compensated for poor genetic endowments, but at high levels of genetic endowment, there was no effect of family socioeconomic status. Many other results in many studies are similar.

The decline in selectivity has had predictable effects that have been clearly observed on several occasions. For example, Denmark expanded its PhD slots and the IQs of enrollees immediately fell:

In the U.S. Army, officer IQs have declined in a fashion largely explained by increased college enrollment:

Universal screening led to more gifted children being discovered in an American school district, but at the same time, those who were discovered were less intelligent than those students already known to be gifted.² Finally, McGue et al. (2022) showed an IQ-by-education distribution that may surprise you:

They noted:

Although most individuals with IQs ≤ 90 in both generations did not complete a college degree, the rate of college completion in this group increased approximately 6-fold (in men) and 10-fold (in women) between the parent and offspring generations.

With this—and more—evidence in hand, we have a strong prior. But we also have more direct evidence. For example, norming datasets—which are intended to be population-representative—show continual declines in the IQs of people at higher levels of education relative to the normative means.³

The means declined and the variances increased.

Thanks to Wicherts et al. (2004) we also have data from the norming samples of the Dutch Differential Aptitude Test (DAT) from 1984 and 1995. The DAT’s norming samples were stratified by education, with a medium-low, medium-high, and high-education cohort for each year. In the Netherlands, 93% of the size of the 1984 cohort of qualified secondary school graduates enrolled in university versus 109% in 1995. Between total cohorts, there wasn’t much change and there was no change in latent g. However, for the educationally stratified cohorts Wicherts et al. worked with, the medium-low cohort’s showed an IQ loss of 2.85 points, the middle cohort showed an increase of 0.30 points, and the high cohort showed a decrease of 4.82 points. Model fits for these cohorts using Wicherts et al.’s model are given in this footnote.⁴

For the medium-low cohort, the vocabulary subtest was biased in favor of the later group and the verbal reasoning subtest was more variable in the later cohort too. The latent variances for g and verbal ability declined substantially between cohorts while abstract reasoning became more variable. Abstract reasoning increased substantially while g declined. In the medium-high cohort, the vocabulary and numerical ability subtests were biased in favor of the earlier cohort and the later cohort had higher verbal ability, but abilities were otherwise equal. In the high cohort, numerical ability was biased in favor of the later cohort and language use was biased in favor of the earlier cohort, while g didn’t differ and the later group lost substantial amounts of verbal and abstract reasoning ability.

Bias-corrected changes in mean IQ scores were -3.37 points for the medium-low cohort, +1.16 points for the medium-high cohort, and -3.78 points for the high cohort. Because the mean overall didn’t move much, we know selection across education levels matters, and it produced a pattern where losses were concentrated among those with low and high levels of education while changes in the middle were more muted.

Large-scale registry data from Norway shows a similar temporal pattern: between the 1950 and 1991 birth cohorts, the education-intelligence correlation continuously declined.

As more and more people have obtained educations, the meaning of a given level of it has changed. Where a high education level used to strongly imply that someone was highly intelligent, it now no longer does.⁵

---

Who’s Smarter, Germans or Greeks?

Among major European nations, who’s the most trustworthy? Who’s the most arrogant? Who’s the most compassionate? The answer depends on who you ask. When Pew asked in 2013, here’s how it turned out:

Pew (2013)

Germans sure are trustworthy—unless you’re Greek—but they’re not really that compassionate, are they? It’s hard to measure the truth of this sort of national stereotype, so let’s use a hard measure: intelligence. If we ask which Europeans are most intelligent, the answer is likely to be Estonians or the Swiss, and the Germans are certainly up there too.

Or at least, the Germans would have been before they made the mistake of reducing the time people spent in school by a single year. That’s the conclusion one might gather if they believe Bergold et al.’s 2017 analysis of the G8 school reform.

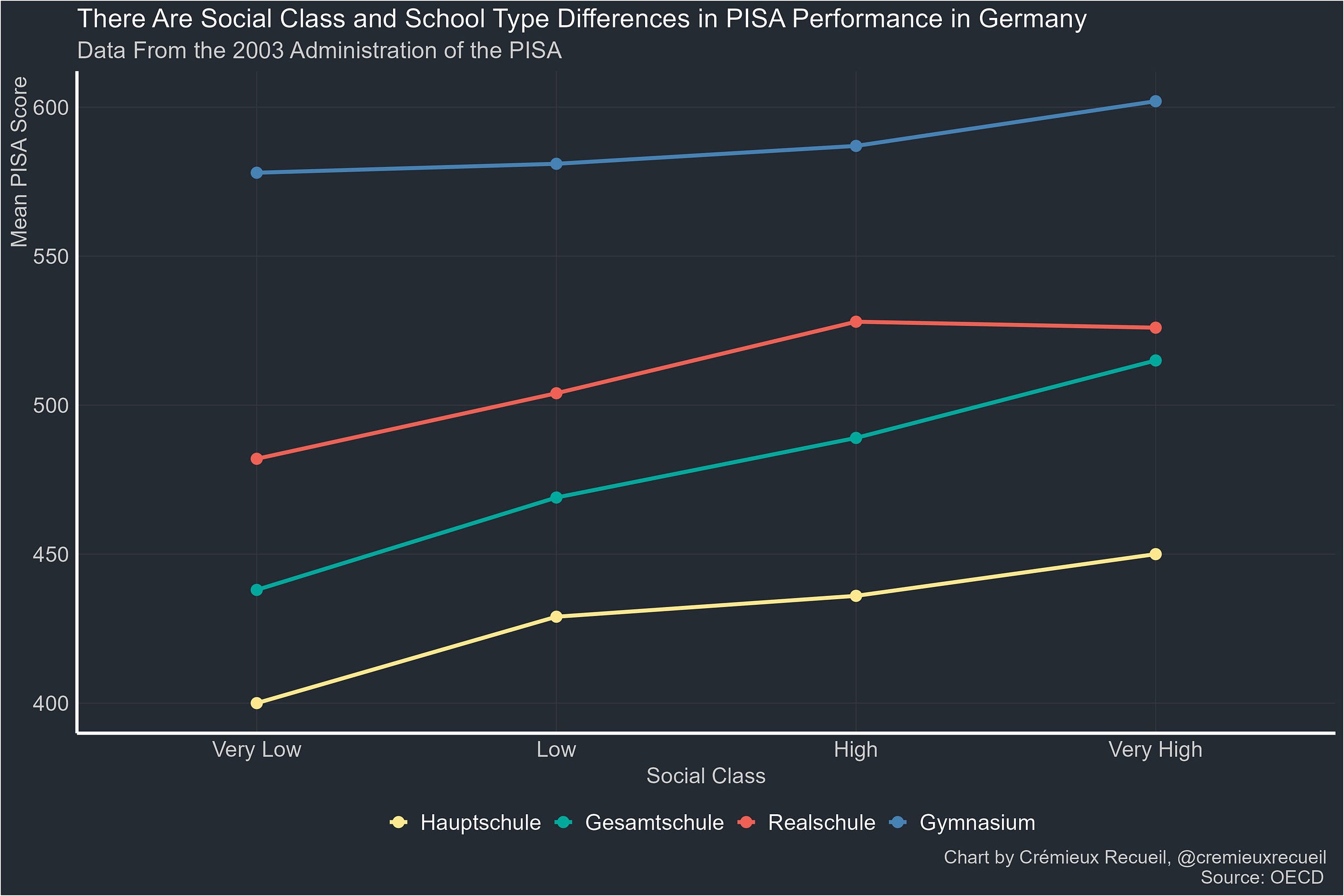
The reform Bergold et al. concerned themselves with is an interesting one. For background, the German secondary education system is tracked. At the lowest level you have the Hauptschulen, schools for general learning which can be attended by anyone who attended a German elementary school. A level up from that are the Realschulen, which are generally gated by a test. Beyond the Realschule is the Gymnasium, the academically focused university preparatory schools. There are differences by Länder and some distinguish between the Hauptschule and the Gesamtschule (generally nonselective comprehensive schools), but that’s beyond the scope of this discussion. Using pre-reform PISA data from 2003, we can see how these schools are intellectually stratified:

The length of time students spend in secondary school differs by the type of school. The G8 reform reduced the length of time people spend in Gymnasium from nine to eight years. Students were expected to complete the exact same curriculum, but they were simply told to do so in a shorter amount of time with how that’s managed varying by state. In Berlin, Brandenburg, and Mecklenburg-Vorpommern, the reform reduced school lengths from seven to six years, and in Saxony and Thuringia, the reform did nothing since they already had shorter school lengths since 1949.

The response to the reform has been tepid. The state of Bavaria ran with it between 2012 and 2018 before returning to the earlier G9 curriculum. In Lower Saxony, they ran with it from 2011 until 2019 before doing the same. North Rhine-Westphalia shifted from G9 to G8 in 2012 and plans to return to G9 starting in 2026. In Rhineland-Palatinate, only some schools were ever transitioned to G8, and they only started doing so in 2016. Some states had briefer contact with G9. For example, Saxony-Anhalt had G8 from 1949 to 2000, switched to G9, and then switched back to G8 in 2007.

Bergold et al. investigated the effects of this reform in two studies. The first involved comparing students tracked into G8 (n = 81) and G9 (80) at different ages in a school in North Rhine-Westphalia. The G9 students were tracked in 2004 and the G8 students were tracked in 2005, allowing both to be assessed at the same grade level in 2010. At the time of assessment, the G9 students averaged 16.39 (σ = 0.49) and the G8 students averaged 15.16 years old (0.37).

Using the Berlin Intelligence Structure Test, it was found that the G8 cohort averaged 0.59 d below the G9 cohort—almost nine whole IQ points! That is an unbelievably huge amount of change for having one year less education. The difference was confounded with age, but the authors looked and found that correcting for age didn’t do much, reducing the gap from 0.59 to 0.51 d, or from almost nine to almost eight IQ points.⁶

I don’t believe the age correction was credible. After all, the Millennium Cohort Study is available to us, and it shows a major birth month effect similar to this one, which is entirely an age in cohort effect that can be explained by an interaction, but not by linearly residualizing for age. Bergold et al. cited a study from 1995 to argue against testing for an interaction. I can’t access that study, so I don’t know how credibly it addressed the issue, but I do know the problem shows up in data that everyone can access, so why not at least test it?

With Bergold et al.’s tiny sample, correction might not have been worthwhile anyway. Interactions require a lot of power to test, so sometimes you just won’t be able to answer your questions with small samples, and there was certainly no way to take out more meaningful fixed effects with the limitations they had to work with. The second part of the article may have been a bit better though.

In Bergold et al.’s second study, they compared two G9 cohorts (total n = 204) sampled in 2007-08 and two G8 cohorts (244) tested in 2012-13 using the Intelligence Structure Test 2000 Revised, in schools in North Rhine-Westphalia. A colleague was given the data and they tested it and confirmed the authors’ findings directionally: after correcting for age and sex and restricting the means of the verbal and numerical group factors, the earlier G9 group had 0.34 d higher g—German students were evidently five IQ points less intelligent when tested a mere five years apart!

If we go with the authors’ suggested estimate of 0.72 d lower g, we’d be forced to concede that it seems within five years, the German mean for Gymnasium students had fallen by the equivalent of the German-Greek gap, or about two-thirds of the gap between White and African Americans. That’s enormous.

But it’s also probably not real.

Remember: when we expand the pool of those receiving educations, we reduce the intellectual advantage associated with education. The standards for entering Gymnasien declined and the enrollment in them increased in this period, across reform and non-reform states. The G8 reform either prompted or (more likely) coincided with increased enrollment. In the Fachserie 11, Reihe 1: Allgemeinbildende Schulen – Schuljahr 2009/2010, 28% of precollegiate students were listed as being enrolled in Gymnasium. Based on the Statistiches Jahrbuchs for 2009, 2012, and 2013, it seems the increase over the period was on the order of 50% nationally; as Bergold et al. noted: “In 2012/2013, for instance, 44.5% of the students in the German secondary school system attended the Gymnasium.”⁷

It shouldn’t come as a surprise that so many people criticized the school system around the time of the reform from the angle that Abitur⁸ taking and Gymnasium entry had become too widespread and easy. The reform apparently just coincided with widespread concern over declining standards. Given the average proportion eligible to study at university in 2007/2008 was some 20% lower than the proportion in 2012/2013, we should probably not believe the point estimates from this study represent the effects of G8/G9 attendance but, rather, that they reflect the effects of selection much like the selection into education observed elsewhere. Similarly, the recent estimate that German university students became 4.68 to 5.17 IQ points less intelligent between 2012 and 2022 should be treated the same way.

The studies purporting to show that German Gymnasium and university students have become substantially less intelligent over time due to a reform whose influence wasn’t isolated⁹ or the pernicious anti-Flynn effect are not credible. They suffer from serious potential selection issues.¹⁰ Thankfully, economists love dealing with selection issues, and they have.

---

Credibly Evaluating the G8 Reform’s Educational Impacts

Dahmann (2017) used two cohorts to investigate the G8 reform’s effect. These two cohorts are really great for several reasons. The most important thing is that both are readily downloadable (if you’re European. Sorry non-Europeans!). The samples are also large enough, nationally representative, they contain extensive background details about participants, and they have good measures. The first is the Socio-Economic Panel (SOEP); the second is the National Educational Panel Study (NEPS).

The SOEP had the same cognitive test used in Bergold et al.’s second study. That’s useful! We know the psychometric characteristics of that battery were good, and we can confirm the same thing in the SOEP. In this cohort, the group being analyzed were individuals observed in the 2006 through 2013 waves who attended Gymnasium. As a result, there were 723 students in the sample, of whom 288 were affected by the reform. Additionally, pre-reform socioeconomic and demographic variables including migration background, sex, age, teacher recommendations after elementary school, parental education, work status, occupation, and family structure were all controlled for.

The NEPS used a lengthy cognitive test covering mathematics, perceptual speed, and reasoning. Mathematics was measured with a standard achievement test, perceptual speed was measured with a picture symbol test, and reasoning was measured with the Raven’s matrices. Migration background and sex could be controlled in addition to socioeconomic status variables like books in the home, and both parental education and occupation. School characteristics including size, share of students with migration backgrounds, and stress factors induced by the reform were also controlled for. The NEPS sample included 2,128 students sampled in 2013, of whom 1,113 were affected by the reform.

Estimation with the SOEP dataset involves comparing individuals who entered school in a given state in given time periods where they would be affected or not affected by the reform, with all the aforementioned controls and additional state and year of birth dummies. Estimation with the NEPS dataset involves comparing individuals in different states in the same school years, who ended up in those school years because of the timing of the reform. So the comparison will be between individuals who did an additional year of schooling versus those who had more intense schooling for one less year.

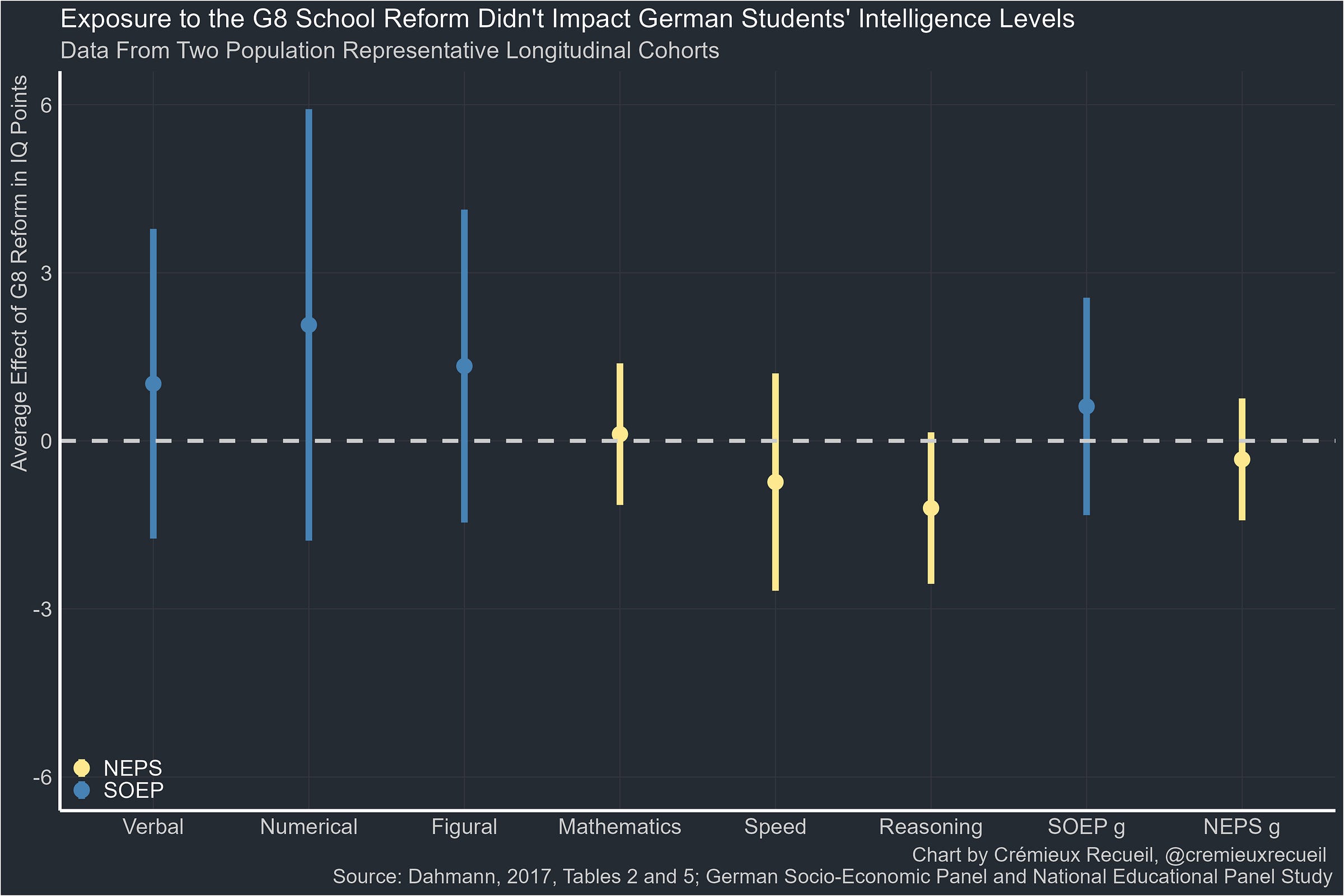
Because I have access to both datasets, I will show the original estimates in addition to estimates for a single-factor latent g, noting that I could constrain the effects on latent g to 0 to improve fit. Effects are rescaled into the IQ metric. Here are the estimated effects of reform exposure:

The effect is estimated to be approximately nothing. There was no grand collapse in student abilities, nor was there a major increase due to schooling intensity rising to allow students to learn the compressed curriculum. This also replicates with other publicly available data.¹¹

Andrietti and Su exploited the staggered implementation of the G8 school reform across time and states to provide difference-in-difference estimates of the effect of the reform on student PISA scores. That’s a simple and plausibly causal design! They used all the standard controls—sex, age, parental education, only child status, immigrant status, foreign language status, etc.—and also had school-level controls—enrollment, female percentages, urbanicity, private school status, student-teacher ratios, teacher and resource shortages, etc. I extended this analysis by using g factor scores from a higher-order model of the PISA battery, consistent with the interpretation of PISA scores as reflections of g made by Pokropek et al. on two occasions.

The transition years were 2001 for Saarland, 2002 for Hamburg, 2003 for the 5ᵗʰ-9ᵗʰ grades in Sachsen-Anhalt, 2004 for the 5ᵗʰ-6ᵗʰ grades in Niedersachsen, the 5ᵗʰ-9ᵗʰ grades in Mecklenburg-Vorpommern, 10% of Hessen, Bremen, the 5ᵗʰ-6ᵗʰ grades in Bayern, and Baden-Württemberg, 2005 for Nordrhein-Westfalen and 60% of Hessen, 2006 for Brandenburg and Berlin along with the remaining 30% of Hessen, and 2008 for Schleswig-Holstein and Rheinland-Pfalz. The PISA examinations in Germany in this time involved additional, expanded samples, so there ended up being a lot to work with, and data from 2000, 2003, 2006, 2009, and 2012 was used, so there was plenty of identifying variation.

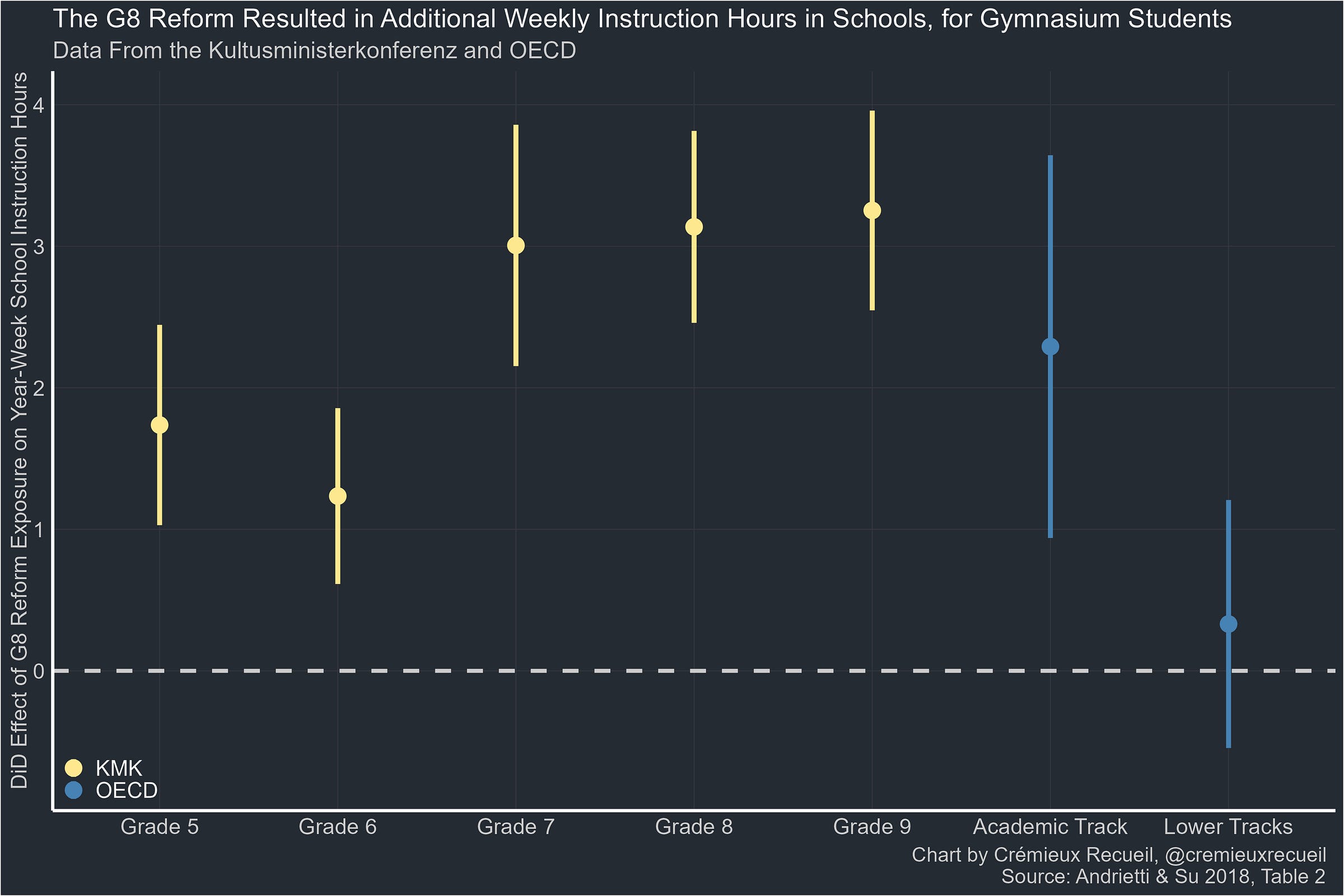
First, consistent with the idea that the G8 reform should have increased the intensity of education, Kultusministerkonferenz (KMK) data on weekly instructional hours showed that the G8 reform was associated with more instructional time. Consistent with this, self-reported instructional hours were greater in the PISA data as well, but only for those affected by the G8 reform: Gymnasium (i.e., academic track) students, not lower track students

So how well did the G8 reform-exposed kids do relative to the non-exposed? They were not significantly more intelligent despite having a sample size of over 30,000 students. They did have significantly higher latent science and reading ability, but not mathematical ability. Since the gains to mathematics were marginally significant in Andrietti and Su’s specification and nonsignificant in mine, that makes sense.

Here are the results for three different specifications. The first is the main specification, the effect of the G8 reform on the scores of Gymnasium students’ PISA performance by subtest. The second is the placebo specification, where the cohort immediately preceding the exposed one is used instead. The final one is the effect on lower track students. All values have been rescaled into the IQ metric.

The results for lower track students are noisier, but given the placebo result, it’s clear that we should consider them to be more similar to the placebo result than they are to the main specification. The main specification showed clear gains to reading and science scores, with less persuasive evidence for an effect on mathematics, but for the placebo Gymnasium and lower track students, the estimates were clearly indistinguishable from zero. At the very least, the G8 reform was not harmful.

Perhaps the most interesting result of the G8 reform is a potential Matthew Effect, where the highest-performing Gymnasium students might have done better than the lowest-performing ones. Stratified by performance, the G8 effects look like this:

This result isn’t especially strong because the standard errors are so large, but it’s consistent with a few things worth noting. The most important thing to note is that there’s no evidence that the G8 reform hurt weaker students. The second is that it speaks to how, even if the G8 reform worsens inequality in student learning, that’s OK! On average, the reform was still beneficial, but if some people fall behind as a result, they’ll still have that extra year to repeat a grade and as a result, the worst outcome for them would be ending up where G9 students would have been anyway in terms of age progression.

With each of these results—from the SOEP, NEPS, and PISA—in hand, I believe we can confidently reject the results of Bergold et al.’s analysis and suggest quite confidently that they were driven by selection that they didn’t account for. With the SOEP and PISA results, we see that when it comes to measured achievement, the reform is probably slightly beneficial. The NEPS result suggests that, if there’s a duration effect, it’s at least balanced by the intensity effect, resulting in no net effect on student learning, much less intelligence. The well-controlled evidence all seems to agree: shortening school lengths in Germany was not harmful. We shouldn’t fear it, nor should we believe poorly controlled results showing massive declines in actual student intelligence in the first place.

---

Explaining Ontario

Ontario, Canada adopted a G8-like reform, where they reduced high school durations from five to four years in length. This has been widely panned as a failure.

Krashinsky found that four-year high school graduates aged 18.25-19.25 had mean university management course GPAs of 2.39 versus five-year graduates’ 2.72. In the age range 18.5-19, the means were 2.27 and 2.80. Morin used a much larger sample and grades from many more courses and found generally nonsignificant differences, but still observed a deficit favoring the five-year graduates, to the tune of 2.3 points on a 100-point scale.

These effects of reducing high school duration were consistent in direction, but they were very modest and not altogether concerning. Regardless, we should still take them seriously. To that end, I think the German results could be informative about the Ontarian ones.

The G8 reform maintained the curriculum while reducing the time in school, but the Ontario reform simply reduced the length of school and cut back on the curriculum to make room. As a result, they failed to raise the intensity of education to compensate for reduced time in it. The seemingly balanced impact in Germany might be ascribed to the necessarily increased intensity of education of their reform, and Ontario could take notice of that critical distinction.

---

How Little School Can We Have?

There may be more diverse impacts of reducing school lengths.

Using the NEPS, Hübner et al. found suggestive evidence of effects on achievement-related fear and school-related stress differences between boys and girls. Both effects were so small they wouldn’t survive correction for multiple comparisons.

Schwerter, Netz & Hübner found suggestive evidence that reform exposure led to fewer hours attending university classes and on self-study, with larger time gaps between school completion and entering high school (i.e., more gap time). Each effect was marginal and ignorable aside from the roughly 1-to-2-month increase in gap times. Stöver also found that the reform negatively impacted immediate higher education transition rates, but every other transition was positively impacted.

Huebener (not relation to the Hübner mentioned above, presumably) recorded that the G8 reform was associated with ten months less time in school, just shy of the anticipated twelve month reduction, due in part to grade repetition rates increasing by 3.08%, or about a fifth in relative terms. Consistent with girls being the more studious sex, boys experienced an increase of 3.78% versus 2.40% for girls. This finding, however, does not show that there were necessarily more failures, as the increase was largest in the final, Oberstufe, year that students might wish to voluntarily retake to “change their specialist subject choices or to improve their grade point average, for example.” The rates of graduating with an Abitur were also not found to be affected, so the biggest impact was really just students graduating at a younger age.

These and other findings don’t actually seem like they make for a strong case against reducing school lengths.

This is no small issue; these findings matter. Reducing school length means giving people back time as young adults to start their careers, to form relationships, and—critically—to get married and start families. I’ve suggested before that more available time as an adult might be a way of fighting the tempo effect on fertility.

Economists have repeatedly brought up this issue and noted that the case for reducing time in school to recover people’s youth seems to be good. But, if we must have a certain quantity of school as a matter of human capital development, there are other options than holding people back from starting their adult lives. As the German experience shows us, increasing intensity seems capable of balancing the effect of time in education, so why not simply extend school days? In the process, we’d be able to incapacitate youths for longer—combatting the sharp ascent of the age-crime curve—and to fit in more schooling in fewer years, if we really wanted that.

Consider this diagram of Austrian life cycles between 1971 and 2001:

People are spending more of their lives retired, and that’s good. The primary reason is that we now live longer lives than we used to. But we’re also spending more and more of our lives in education, and that threatens the time in the parts of our lives where we really enjoy being adults. Through reducing school lengths—even in combination with higher schooling intensity or earlier starts—we can take back some of those stolen years.

School isn’t what it used to be and the future needn’t be lives spent entirely in school.

1. Notably, in Uttl, Violo, and Gibson’s Figure 6, they show IPEDS data indicating that admissions rates and SAT totals are inversely correlated. As the admissions rate has gone up over the decades, this comports with declining selectivity as a vector through which means have declined.

2. Honorable mention: The increase in in nurses in the Philippines was associated with declining examination scores, but the reason was not unambiguous.

3. If we simply correct all normative means to 100 arithmetically, the extent of the decline is reduced, but doing this is improper, as we would also need to adjust the variances for complete matching. With just the provided summary statistics, that isn’t feasible.

4. Wicherts et al.’s suggested factor solutions were used with added bifactor g factors.

Medium-low:

Medium-high:

And finally, high:

5. After publication, several people inquired as to how tautological this decline was. The answer is “quite.” Consider the most extreme case: we select the top people from the distribution to go to college. If everyone above the 60ᵗʰ percentile goes to university, the mean of undergraduates under normality and with a population mean of 100 and standard deviation of 15 is 114.488. This is our upper-bound.

If a college education is the 60ᵗʰ percentile of the latent education distribution and this education variable is correlated at 0.50 with IQs, then getting to that level is the equivalent of an IQ of 101.875. Beyond that level, the mean IQ is 113.187. If we continue to imagine education is normally distributed with a 0.50 correlation with IQ, we can simulate the mean IQ of the college-educated group in a straightforward way. We’ll use a sample size of 1,000,000 with the standard IQ metric’s mean and standard deviation. The simulation looks like so:

library(MASS)
Sim_Data <- mvrnorm(n, mu = c(mean_IQ, mean_Education), Sigma = matrix(c(sd_IQ^2, sd_IQ*sd_Education*Correlation, sd_IQ*sd_Education*Correlation,sd_Education^2),
     ncol=2))

colnames(Sim_Data) <- c("IQ","Education")

Ed_Quantile <- quantile(Sim_Data[,"Education"],0.6)
A60 <- Sim_Data[Sim_Data[,"Education"]>Ed_Quantile,]

mean(A60[,"IQ"])

With my seed set to 1, the mean IQ above the 60ᵗʰ percentile of the education distribution is 107.256. Now let’s make education binary rather than normally distributed. To do that, we’ll generate a propensity for education that’s IQ by 0.5 plus rnorm() with a standard deviation determined by iteratively searching for a standard deviation consistent with a correlation between a version of this that’s been dichotomized above quantile(Propensity, 1 - Educated_Prop), where the proportion receiving educations is 40%, and IQ of 0.50. That results in a mean IQ for individuals with educations of 109.188. If you want to replicate this procedure or alter it, you can use

while(abs(Cor_Difference) > Tolerance && Iter < Max_Iter) {
     Propensity <- scale(IQ) * 0.5 + rnorm(n, 0, sqrt(1-Param^2))
     Cutoff <- quantile(Propensity, 1 - Educated_Prop))
     Education <- ifelse(Propensity >= Cutoff, 1, 0)
     Corr <- cor(IQ, Education)
     Cor_Difference <- Corr - Target_Corr
     if(Cor_Difference > 0))
        Param <- Param - Step_Size
     } else {
        Param <- Param + Step_Size
     }
     Step_Size <- Step_Size * 0.95
     Iter <- Iter+1
}

If you raise or lower the proportion involved in university, this code will, respectively, reduce or increase the mean IQ of those with educations in lockstep. With this, it’s straightforward to simulate changes over time and to add a declining correlation between IQs and education as the proportion involved increases if that’s something you’re interested in. But I think this has been sufficient.

The short and sweet is that a substantial portion of the decline in the IQs of undergraduate students is likely to be down to simply increasing the proportion of society that enrolls in higher education. Since the correlation has absolutely fallen over time, that’s not all of it, but it’s likely to explain the majority of it. No matter how you ultimately choose to set up this simulation or to work it out analytically, you’ll find the same result because college involvement simply has that great an effect for tautological reasons.

6. Despite this massive gap in intelligence, the G8 cohort had a nonsignificantly higher GPA (d = 0.26). The expected gap given a correlation of 0.40 between intelligence and GPA is -0.24 d. In Study B, the GPA gap favored the G9 cohort by 0.16 d versus an expected 0.34 d given the authors’ reported age-uncorrected gap in general intelligence.

7. Precollegiate and secondary attending can be different quantities. In Schulen auf einen Blick, Ausgabe 2014, Germany’s total 2002/2003 and 2012/2013 Gymnasium I percentages for all students were reported to be 30.7% and 34.4%, with 31.5% and 32.9% for the study’s Nordhein-Westfalen specifically. Nevertheless, there has been an increase in Gymnasium attendance over time, and there are complaints aplenty about that fact in addition to the accusation that classes have become easier and the more poorly justified rumor that no one would hire anyone in the first combined G8/G9 cohort because too many people would be entering the labor market simultaneously since that class was twice the regular size.

8. University entrance examination.

9. Mexico City’s extension of school time from 4.5 to 8 hours amounts to an larger increase in school exposure, and its effect over twelve years might only end up being around a 0.30 standard deviation boost in high-stakes exam scores.

10. The psychometricians have shown that the scores for G8/G9 cohorts are largely invariant and the bias in comparisons of university students over time is present but probably modest. Econometricians do not tend to take heed of the issue of psychometric comparability over time, so it’s lucky we have these studies even if the declines they suggested were probably driven by selection.

11. Incidentally, while I had the NEPS and SOEP data open, I attempted to replicate Kamhöfer & Schmitz’ replication and extension of Pischke & von Wachter’s study for crystallized cognitive skills. I didn’t want to spend time on the school supply analysis so I didn’t go ahead with replication in the SOEP. Nevertheless, their result is consistent with American results: in analyses with pretty basic fixed effects (which many studies don’t have), reforms don’t seem to do much.

The issue with the German cohorts applied to that question is that the answers are imprecise. For example, the confidence intervals for the Hauptschulen result in the SOEP analysis ranged between -0.14 and 0.08, or between losing 2.1 and gaining 1.2 IQ points. In a preliminary re-analysis in the NEPS, the comparably-targeted effect ranged between -0.08 and 0.06, or between losing 1.2 and gaining 0.9 IQ points. These are different from the latest meta-analytic results, but that’s to be expected since they’re better controlled than the typical study included in them.