Correlations and Coin Flips

Or, how should we talk about small effects?

“Variance explained” (r²) is a misleading metric. One reason is that its scale is unintuitive. A correlation denotes the gain in Y if you change X by one standard deviation (SD). The problems that follow if you square that value were explained well by Hunter and Schmidt:

The “percentage of variance accounted for”… leads to severe underestimates of the practical and theoretical significance of relationships between variables. This is because r² (and all other indexes of percentage of variance accounted for) are related only in a very nonlinear way to the magnitudes of effect sizes that determine their impact in the real world.

Or more intuitively:

The ballpark is ten miles away, but a friend gives you a ride for the first five miles. You’re halfway there, right? Nope, you’re actually only one quarter of the way there…. This makes no sense in real life, but, if this were a regression, the "r-squared" (which is sometimes called the "coefficient of determination") would indeed be 0.25, and statisticians would say the ride "explains 25% of the variance." There are good mathematical reasons why they say this, but they mean "explains" in the mathematical sense, not in the real-life sense.

Alternative, intuitive metrics to r² have been proposed. A popular one introduced by Rosenthal and Rubin in 1982 is the binomial effect size display, or BESD. The BESD is an excellent way of conveying how something that explains “only” a small share of the variance in something else can have enormous practical implications. Consider this table:

This table is based on a meta-analysis of psychotherapy outcome studies where psychotherapy “only” explained 10% of the variance in living or dying (i.e., r = 0.32). Per Rosenthal and Rubin, the “table shows clearly that it is absurd to label as ‘modest indeed’ an effect size equivalent to increasing the success rate from 34% to 66% (e.g., reducing a death rate from 66% to 34%).”

Years later, Rosenthal followed up on the BESD and provided more examples of why it was such an important innovation. To wit, the BESD showed the impacts of

• Aspirin on heart attacks (r = -0.034)

• Propranolol on heart attacks (-0.04)

• Serving in Vietnam on alcohol abuse or dependence (0.07)

• Azidothymidine on AIDS survival (0.23)

• Cyclosporine on organ rejection (-0.19) and patient survival (0.15)

Use of the BESD has… shown that we are doing considerably better in our softer, wilder sciences than we may have thought we were doing. It would help keep us better apprised of how we are doing in our sciences if we routinely translated the typical answers to our research questions to effect sizes such as r (and to its equivalent displays) and compared them with other well-established findings such as [the above.]

It’s now years later, so let’s see some other effect sizes in medicine, expressed as correlations:

Link

It’s easy to agree with Rosenthal, or at least with his point: we need better ways to compare effects. Thinking of effects like a coin flip a la Rosenthal is very appealing, But I think the BESD is the wrong way to go about achieving his goal.

---

Simplifications Fail

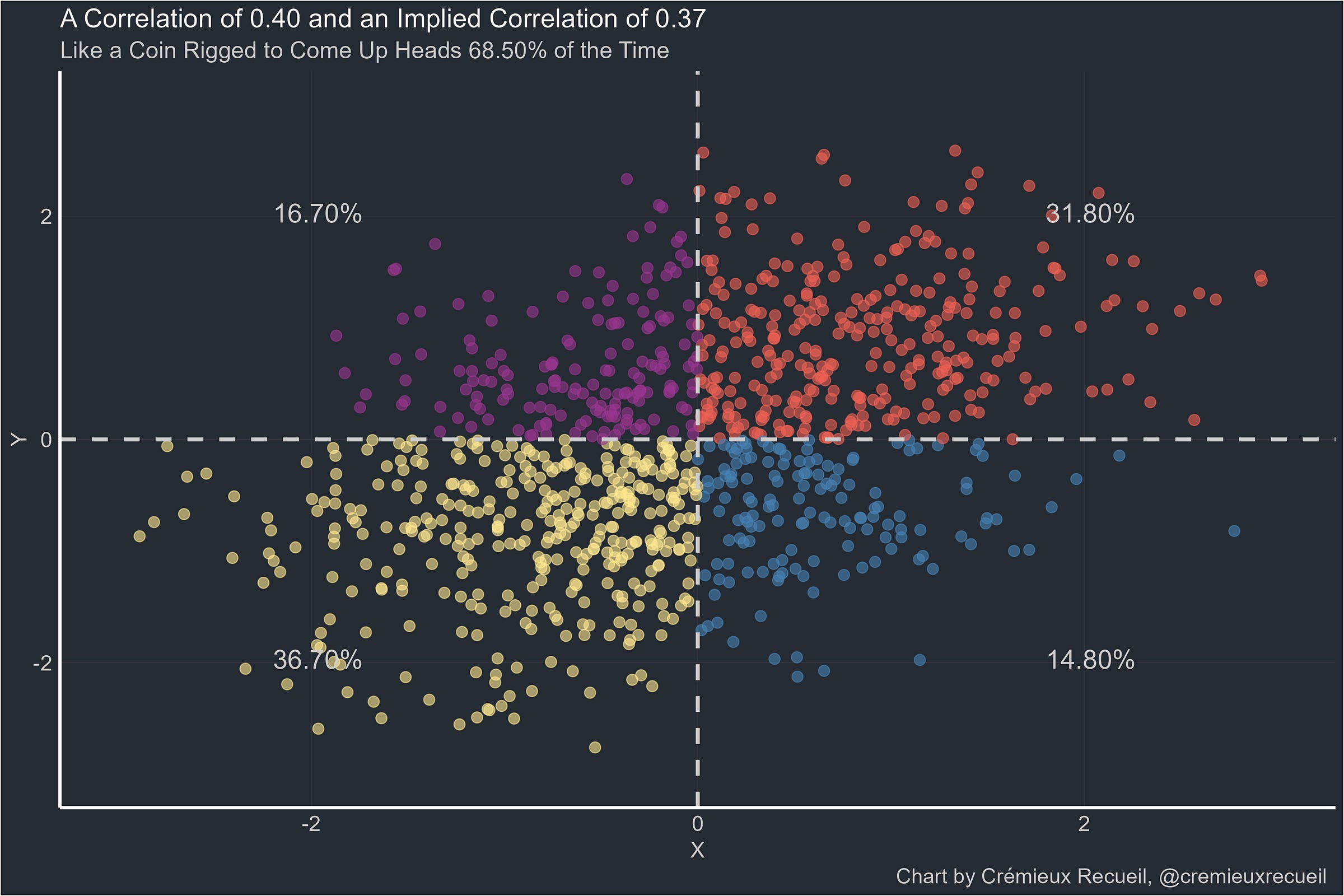
I’m going to generate 1,000 observations of two standard normal variables, X and Y, correlated at r = 0.20. I’ll divide the plotted area by the theoretical medians for both variables and then calculate the BESD-implied correlation using the percentages in each quadrant so that I can compare it to the true, underlying correlation the data was generated upon.

At this correlation, everything looks good for Rosenthal. Now, let’s see a correlation of 0.30:

Everything still looks good, so let’s keep going to 0.40.

It’s at this point that I should make this note: I have tried to pick the closest possible correlation to the target correlation out of seeds 0 to 10,000. That means that the failure to reach 0.40 reflects something real. So let’s see 0.50.

And I’ll finish with this: 0.60.

Is the gap just continuously growing as the true correlation rises? Since that’s easy to simulate by gathering the differences between BESD-implied correlations and true correlations for several thousands seeds, that’s easy to figure out. Here’s the answer:¹

When two standard, normally-distributed variables are dichotomized, they don’t neatly affirm the workings of the BESD. In fact, there are many more conditions where the BESD is not clearly affirmed, such as when tables like the “Only 10%” one shown above instead do not have uniform marginal distributions.²

It’s unfortunate that the BESD doesn’t just work as a way to convert between effect sizes—itself a fraught practice— and intuitive real-world effects, but it’s to be expected. After all, the ‘correct’ statistic to report to understand a relationship or an effect could never just be one, universally applicable value.

---

Effects in Context

Pygmies are very short. That’s the thing they’re best known for, and it’s obvious why.

The reason Pygmies are so small isn’t just poor environments, it’s largely a genetic phenomenon. We know many of the genetic antecedents of small Pygmy stature, but even if we didn’t we know them, the quality of Pygmy environments hasn’t historically been very differentiated from their neighbors, and yet those non-Pygmy neighbors have never been as small. The neighboring Tikar are much more normal!

As it turns out, Pygmies and neighboring groups have interbred. Just as interestingly, pygmies with greater admixture from those neighboring groups tend to be a bit taller.

Becker et al. 2011, Fig. 4.

If we wanted to understand what proportion of the difference was genetic, we could check the correlation between admixture from a taller group and height. If, say, the average Pygmy had 10% admixture from a taller group with an SD of 15% whereas the non-Pygmy population averaged 99% taller group and two SDs taller, the correlation coefficient required to explain the whole mean difference from within the Pygmy group would be 0.34, or an r² of 11%. Just 11%! Not to beat up on variance explained, but if the height gap were one SD, the expected r would be 0.17, or 2.9% of the variance—a very different expectation in squared terms, but a predictably smaller one if we use r.

A “small to modest” correlation can easily explain a major difference in trait means between two groups. That’s one context. Another is liability threshold models.

A now well-known example is that it doesn’t take very much of a relationship between social media use and depression to explain a large, recent increase in depression. In this short animation, we can see that, in a world without social media, the depression rate would obviously be unrelated to social media use since there’s not really any social media use. But, when we add it in and individual differences in social media use take their toll, a “small” correlation of 0.16 (2.6% of the variance!) could increase depression rates to 154% of their level when social media wasn’t around.

---

One Size Does Not Fit All

In 1979, Rosenthal and Rubin remarked that “an appropriate measure of effect size must be sensitive to the context of the data.”

I agree with Rosenthal and Rubin, but shockingly many people do not. There are people who think a correlation of 0.30 is always small, or that significance is dependent on the absolute level of a correlation and nothing below 0.71 is significant. There’s no way to defend those beliefs, but they’re persistent in the public mind.

So if we want to communicate scientific results—and especially those from fields where effect sizes feel “small” to the lay public—, I have one principle to suggest: whenever you have the ability to do so, place effects into an appropriate context before presenting them in terms of well-known, frequently misunderstood effect sizes.

1. That answer was computed with sample sizes of 1,000 and 5,000 seeds. This uses N’s of 10,000 and 10,000 seeds:

2. I’ve discussed what statistic the BESD more clearly corresponds to before.