Why Do We Keep Getting This Wrong?

On the causal effects of education

This is the third in a series of timed posts. The way these work is that if it takes me more than one hour to complete the post, an applet that I made deletes everything I’ve written so far and I abandon the post. Check out previous examples here and here.

---

Does education causally increase income?

The way to answer the question seems obvious: why not simply regress years of education against income?

The problem with doing this is that smarter, more ambitious, and even just healthier people select into going to school longer. One proposed means to overcome this inferential problem is to use identical (monozygotic, MZ) twins. When you do this, you control for practically all of the genetic differences between individuals and you control for the common aspects of the family environment. Theoretically, the result should be a clean causal effect of education on income.

But this assumes twins don’t differ in causally relevant ways. In other words, we have to assume twins are (nearly) equally smart, ambitious, and healthy before they start to pursue school. But the reality may be more like this:

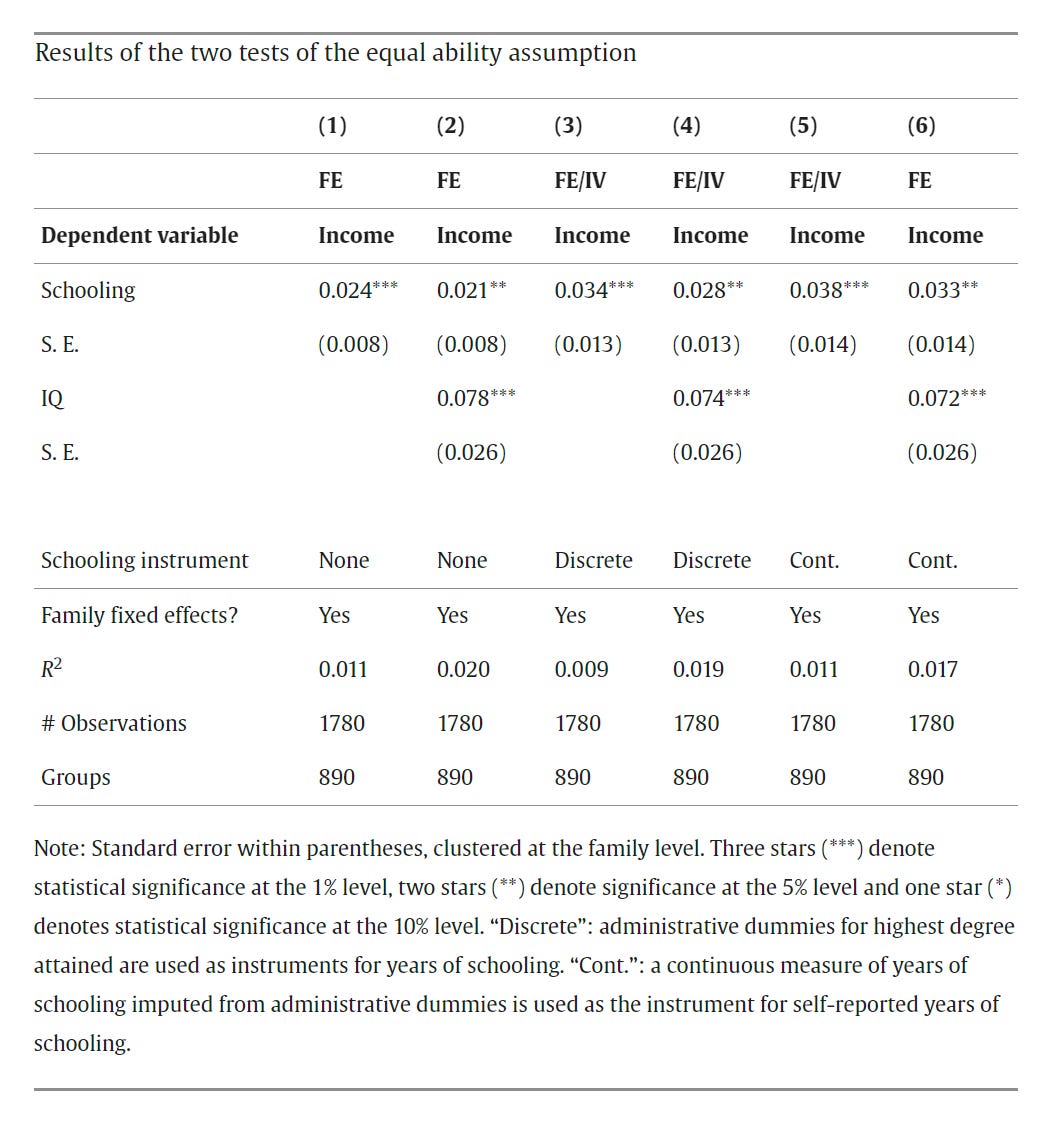
In 2014, Sandewall, Cesarini and Johannesson tested this critical assumption of twin control models—that twins don’t differ meaningfully. Their result was a strong disconfirmation of the idea: differences in IQ between identical twins significantly predicted differences in income net of differences in schooling.¹

Sandewall, Cesarini and Johannesson 2014, Table 2

That result with identical twins showed that the phenotypic differences between them weren’t just noise: they were real, probably causally efficacious differences, that had an impact on the world, so we couldn’t simple assume a significant result in a twin control meant we were identifying a causal effect. It’s true that, in this case, the estimated effect of schooling wasn’t significantly changed by including an ability measure, but in a different social system, like one where there’s a lower level of mandatory education, perhaps that wouldn’t be the case. My point is that designs have assumptions, and their violations can matter if the goal is to make causal inferences.

If we move a step back from the phenotype, to the genotype we lose the ability to do analyses with identical twins as controls. They just don’t differ meaningfully genetically in most cases, so there’s no way to use them. But using fraternal (dizygotic, DZ) twins, we can check if polygenic scores still predict different outcomes between them. When people do that, the result is like this: genetic differences between fraternal twins in educational attainment-related polygenic scores still predict differences in educational attainment, GPAs, IQs, and “soft” (i.e., “noncognitive”) skills.

Willoughby 2020, Figure A.14

We can still milk the twin data further. It’s well documented that differences in brain sizes cause differences in intelligence. This is true in the general population, between siblings, between fraternal twins, and even between identical twins.

Link

So in short, yes, siblings differ, and yes, those differences matter for their human capital and what results from said human capital.

The answer to the headline question is also probably yes, schooling probably causally increases incomes. But with this data alone, I’m not incredibly confident about that answer because, while we might be able to see a robust effect of schooling on incomes within twin pairs controlled for their IQ differences, measurement error in IQ could lead to too little attenuation of the estimated effect of schooling, and other differences between siblings remain uncontrolled, like those in noncognitive skills.

---

Plenty of People Don’t Recognize This Problem

A new preprint on the effect of education on cognition has just come out. The study used the Indonesia Family Life Survey, a large, longitudinal survey that contains sibling data. The way the authors inferred a causal effect of education on intelligence was by comparing the adult IQs of siblings discordant for education with a variety of early-life observed variables controlled.

But as we just saw, differences between siblings can predict differences in IQs, educational attainment, and so on. This was their design:

That’s not good because preexisting IQ (and other!) differences go into the box labeled “Differences in Schooling Between Siblings.” The design is shot and it could only have coincidentally gotten the correct answer—we just can’t tell.

The authors tried to get around this inferential issue by showing that a negative control was unrelated to educational differences between siblings, but this left a lot to be desired. The negative control was that they showed that the cross-sectional relationship between height and education didn’t hold up within siblings, so because that relationship allegedly wasn’t contaminated, we’re supposed to believe the IQ sibling control wasn’t either.

That line of reasoning is not convincing. The differences in trait etiologies render the test uninformative at best because height might simply be related to education for different reasons than IQ is related to education. There’s no reason the null for one finding should act as an affirmation of another test’s alternative hypothesis. Other datasets support this.

In the U.K. Biobank (UKBB), standing height and the UKBB’s fluid intelligence score correlate at r = 0.12. Standing height and degree attainment also correlate at 0.12. The fluid intelligence score correlates with degree attainment at a significantly higher 0.32. The genetic correlation between standing height and degree attainment is 0.23 versus the much higher genetic correlation between the fluid intelligence score and degree attainment of 0.71, and the—also significantly different—genetic correlation of 0.18 between standing height and the fluid intelligence score. There’s more than enough room for the negative control to be irrelevant, but the same result also didn’t replicate in the UKBB. Since the scenarios dramatically differ and fluid intelligence measure was assessed late in life, that replication failure couldn’t be informative about whether the negative control in the Indonesian study tells us anything even if it wasn’t a failure.

So we’ll have to turn to a dataset with a measure of intelligence that preceded later education, the National Longitudinal Survey of Youth (NLSY). In the NLSY’s 1979 cohort, educational attainment is related to early-measured IQ scores within families (B = 1.93, p = <2e-16) and so is sex- and age-corrected height (0.089, 0.002). IQ clearly affects subsequent education to a substantial degree and, while it’s doubtful that education affects height, if we accept the Indonesian study’s identification method, then we would be forced to conclude it does. More realistically, height indexed other things of import for educational attainment between siblings and the negative control was just ill-conceived.

But the negative control result wasn’t meaningful in the first place. Take a look at the results and think about what stands out.

Zhang, Frankenberg and Thomas 2024, Table 6

At baseline, there’s a significant difference in heights for males (p = 0.01), but not females (0.37). There are good theoretical reasons to split the sample by sex: height varies substantially by sex and educational norms may differ across sexes. That split is theoretically justified, but let’s imagine we have no theory. Is it statistically justified? By that I mean, is the difference between the male and female gaps significantly different? A gap of 0.25 points with a standard error of 0.092 versus a gap of 0.07 points with a standard error of 0.078 is not significant (0.14).

With background variables controlled, the gap shrinks down to 0.15 for males, and it’s no longer significant (0.08). For females, it’s not significant and it’s reversed (0.48). Adding in sibling fixed effects, there are no significant gaps (0.83 for males and 0.24 for females).

But is the negative control really showing us a difference between the baseline and when sibling fixed effects are included? Maybe, but I don’t believe it was informative because the difference in the gaps for males and females are not significantly differentiated between baseline and sibling fixed effects models (0.08 for males and 0.79 for females). In other words, the negative control just wasn’t informative.²

---

What If Education Did Improve IQs?

Let’s imagine we had a design with identical twin pairs, we controlled for early IQs, and later IQs were still influenced by education attained in the interim. That would be a solid improvement in design, but still not an informative result, because we have to move beyond econometrics into psychometrics to grasp what education affected.

To understand what I mean, think of IQ scores as rubbish bins.

IQ scores vary because of between-individual differences in intelligence, in specific abilities like skills at mathematics or vocabulary, due to differences in motivation, because of things specific to subtests (Sarah might be especially good at pressing buttons quickly because she played a lot of button-pressing videogames), and because of bias (someone might have seen a test answer, people might be differently familiar with the format of a test, or people in a sample might not speak the language of the test equally well, etc.).

An effect on IQ scores doesn’t tell us what we actually want to know. We want to know if intelligence has been enhanced³, because that’s what’s interesting. It’s not meaningful if people merely improved at test-taking, because that’s unlikely to result in improved real-world outcomes. While jobs may be IQ tests, they are not literally IQ tests, and expecting improvements in terms of IQ scores alone to impact on-the-job performance in a scenario where ability doesn’t change is asking for a lot that’s not likely to be delivered.

A small number of studies have looked at what aspects of test scores education affects using longitudinal data, and they have not come away looking like they support an effect of education on intelligence itself. The best published example of this comes from Ritchie, Bates and Deary. They found, controlling for Moray House Test scores measured early at age 11, the effect of education on intelligence test scores at age 70 was relegated to specific tests, not general intelligence, g.

Ritchie, Bates and Deary 2015, Figure 4

Unfortunately, this study lacks two things: a test of measurement invariance, and a test of what those educational gains predicted. Because the sample was at retired age, it might not have been reasonable to ask for the latter, but the former still could have been tested.

A replication of this study looked at the effects of a university education on intelligence test scores in a sample of Americans, many of whom were drafted to fight in Vietnam. The effects of education were also found to be on specific subtests, not g, and the educational boosts to those tests didn’t predict higher incomes, but obtaining more education did. In other words, the income-boosting effect of education wasn’t mediated by boosting test scores, it was separate from that effect. This replicates the result McGue et al. recently reached, where they also found that education was related to benefits to socioeconomic status net of IQ.⁴

Now, this replication also didn’t test for bias, but they provided all of their raw data, so I was able to do a multi-group confirmatory factor analysis of it. I found that the education-affected subtests were biased when comparing samples with only high school educations or less versus those with more than a high school education (any amount). In other words, the theoretical concern that IQ boosting might not be valuable and that it might not even be intelligence-boosting is a legitimate one that needs to be taken seriously, because test results are rubbish bins.

---

Other Designs Remain Problematic

In 2018, Ritchie and Tucker-Drob showed that education boosted IQ scores in a meta-analysis of studies exploiting school age cutoffs, policy changes, and differences in education related to IQ after controlling for earlier measures of intelligence. The effects they meta-analytically observed were quite large!

Ritchie and Tucker-Drob 2018, Fig. 2.

Each of these types of designs suffers from the common issue of not knowing whether the effects are due to real changes in intelligence or other abilities and not knowing if the effects are due to bias, but they each have their own problems besides that.

The “Control Prior Intelligence” studies are like the Ritchie, Bates and Deary study and its replication. But here’s a problem: are developmental trajectories of ability independent of subsequent education? If they are not, then the prior intelligence control might conflate developmental gains with educational gains.⁵ This is a genuine concern, because more intelligent people do take longer to develop and they both start puberty later and show differences in the rates of change in the variance components underlying intelligence scores by age, suggesting they reach their IQ asymptote later.

Link

Policy change-based designs are probably the least problematic of the three, and they are still problematic for another unique reason: the Flynn effect! The Flynn effect can generate rapid, nonlinear changes in IQ scores between cohorts that even show up within families.

Bratsberg and Rogeberg 2018, Figure 2

Thankfully, this is easy to overcome for plenty of policy changes because there are often people who weren’t exposed to the policy change whose scoring trends can be compared with the exposed groups to adjust their regression discontinuity estimate. Unfortunately for us, doing that is rare and doing it with appropriate psychometric modeling is unheard of.

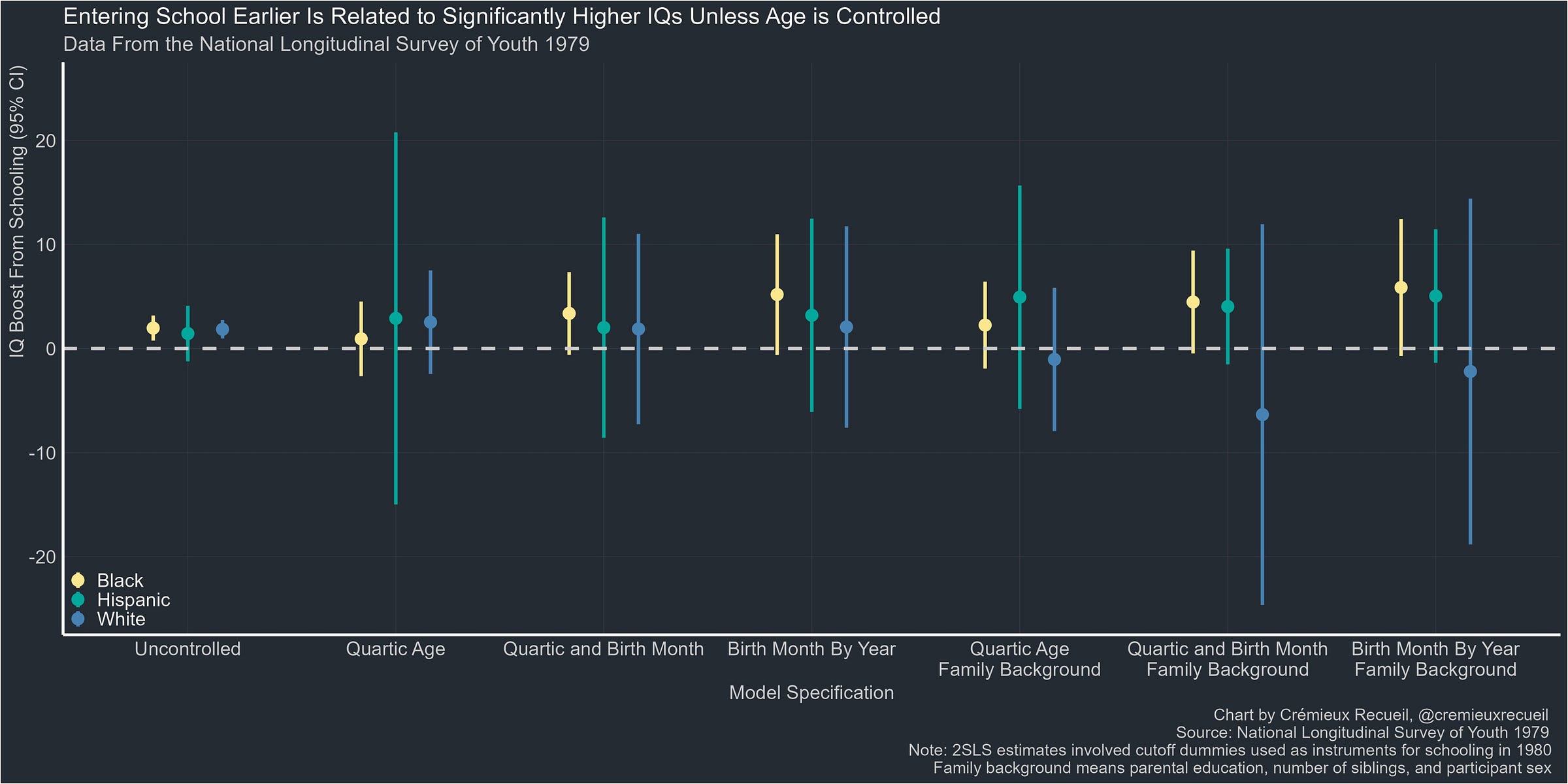
The school-age cutoff method depends on how age is controlled, and it’s rarely controlled well. When done using variation across, say, states, it’s rare to see year of birth effects allowed to vary across regions. When that’s done, positive effects of education are sometimes rendered nonexistent. I’ve checked how this holds up for IQ in the NLSY 1979 (and some other datasets), and the result is frequently just odd.

Link

It’s also not clear how much this matters. Does it fade out? When do we hit diminishing returns? Does this really imply we should keep kids in school longer? And as with the other designs, are we sure these effects are really ability-related? In the NLSY 1979, the answer to the last question is “no”—the gains are not gains to general intelligence, and man are they noisy.

Another proposed method for identifying causal effects of education on cognition is to rely on a fallacy that really should be obvious.⁶ The fallacy is that a polygenic score is a complete control for genetic endowments, so controlling for it eliminates genetic confounding. Many studies, rely on this belief; they regress schooling on an outcome controlling for a polygenic score, and they find that schooling remains significantly related, but they never seem to mention that the polygenic score isn’t a complete index of the genetics they’re trying to control for.

To get at why this is so obviously bad, consider what would happen if we used different iterations of the educational attainment polygenic score from differently-sized GWAS. EA1 would lead to less reduction in the effect of schooling than EA2, which would lead to less reduction than EA3, which would lead to less reduction than EA4, because each iteration progressively explains more genetic variance in education. But worse than this, these analyses assume the genetic predictor they’re controlling for is related to education in each cohort similarly, whereas we know that the genetics underlying many traits must have changed over time. Education is probably one of the best examples of this because the increase in education over the generations has greatly changed what the trait means.

But even if the scores worked the same way all the time and they indexed all the relevant genes, theoretically, what is education net of an education polygenic score anyway? The effects of education we’re familiar with are genetically confounded. Does unconfounded education have the same impacts as cross-sectional education? I doubt it, since, for example, we know that more heritable IQ subtests are more g-loaded. I have to imagine a ‘deconfounded’ education effect would be an effect on something besides g when it’s computed from this design. Or in other words, psychometric modeling is an inescapable requirement.

---

Why Are We Stuck With Either/Or?

The Indonesian sibling control study used a fine design given a set of assumptions that were unlikely to be met. But even if those assumptions had been met, the psychometrics of the piece were too poor to make the sorts of conclusions the authors wanted to.

I don’t want to single out the paper’s authors. Their sort of neglect isn’t unique to them. I’ve also covered a study that did fine on the psychometrics, but used a poor design that rendered the psychometric modeling uninformative. Some relevant data in that case was publicly accessible and the conclusions of the psychometricians were the ones that came up wanting, whereas the econometricians—by dint of getting a null—got the answer that was more likely to be correct.

It’s very rare to see a study that combines both a good design that’s understood appropriately and appropriate psychometric modeling. As a result, few studies in this area can reach the conclusions they want to reach. I can’t see any good reason why anyone who has the data required to deal correctly with the econometric or psychometric side of things only deals with one or the other, so why does that happen? After talking with a lot of people about it, I’ve come to the conclusion that the reason is just that the disciplines are siloed. The econometricians don’t think about the psychometrics of questions, and the psychometricians aren’t aware of potential design problems with their studies.

To understand how education affects anything causally, we can’t neglect either ‘metrics.

1. This result was robust to excluding the top 5% most differentiated twins (i.e., the most likely to be misclassified dizygotic twins), using only twins who both completed high school, using the first principal component of four cognitive subtests instead of a stanine score, exchanging schooling instruments and regressors, setting thresholds for income, trimming twin pairs with more than a four year gap in schooling, and using a proxy for ability in the form of birth weight (although this last control’s result was just marginally significant).

2. Their sibling fixed effects results for males showed p-values of 0.01 and 0.003 for quantitative and abstract reasoning, respectively. For females, they found p-values that were highly significant (1.05e-08) and nonsignificant (0.30), respectively. For the height negative control, the results were supposed to differ from baseline and they did not; for this test, they were supposed to be non-null, and they generally were non-null but they could differ from baseline, so the education-IQ relationship held up within sibling pairs.

3. We might want to know if a specific skill that broadly affects performance in a given domain was affected, but since those don’t tend to have much predictive power when they’re evaluated well, I’m not going to deal with that in this article.

4. This still does not necessarily say that education is responsible for socioeconomic boons. To get there, we would at least need something like a control for noncognitive skills—which it might still index after controlling for IQ. McGue et al. did have that, and they did a within-monozygotic twin comparison and found effects on occupation and independence, strongly suggesting that education is causal for improved socioeconomic outcomes, though effects on income and legal problems were not significant.

5. This is why looking at adult education after an adult IQ test is necessary. It is also why a control prior IQ result with identical twins who had their IQs measured early in time might be confounded with development too (albeit generally with a different direction of effect), even if it should be much less confounded than in the cross-section. This is also a legitimate concern, as we see things like catch-up growth in twins; we know it’s possibly concerning for physical traits and we have no reason to think it isn’t thus true for psychological ones too.

6. Another method that I did not have time to address in this piece is Mendelian Randomization. If you want to use that method, I hope you get lucky and your genetic instrument truly has an effect that’s mediated solely by the phenotypes of interest to you, or you could be out of luck.